
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Điều kiện 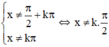
tanx – 2.cotx + 1 = 0
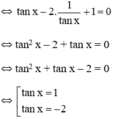
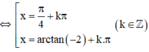 (Thỏa mãn điều kiện).
(Thỏa mãn điều kiện).
Vậy phương trình có tập nghiệm
{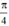 + kπ; arctan(-2) + kπ} (k ∈ Z)
+ kπ; arctan(-2) + kπ} (k ∈ Z)

cotx - cot2x = tanx + 1 (1)
Điều kiện: sinx ≠ 0 và cosx ≠ 0. Khi đó:
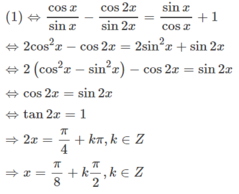

Điều kiện của phương trình: sinx ≠ 0, cos ≠ 0, tan ≠ -1.
Biến đổi tương đương đã cho, ta được
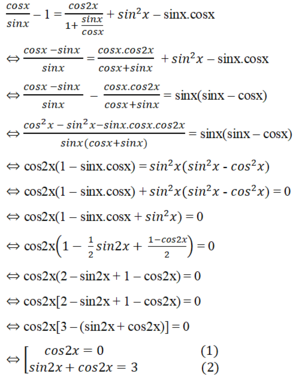
Phương trình (2) vô nghiệm vì |sin2x + cos2x| ≥ √2.
Phương trình (1) có nghiệm 2x = π/2+kπ,k ∈ Z
⇒ x = π/4+ k π/2,k ∈ Z.
Giá trị x = π/4+ k π/2, k = 2n + 1,
với n ∈ Z bị loại do điều kiện tanx ≠ -1.

a) Vì \(cotx = 1\)nên phương trình \(cotx = 1\) có các nghiệm là \(x = \frac{\pi }{4} + k\pi ,k \in \mathbb{Z}\).
Vậy tập nghiệm của phương trình là: \(S = \left\{ {\frac{\pi }{4} + k\pi ,k \in \mathbb{Z}} \right\}\).
\(\begin{array}{*{20}{l}}{b){\rm{ }}cot\left( {3x + 30^\circ } \right) = cot75^\circ }\\{ \Leftrightarrow \;3x + 30^\circ = 75^\circ + k180^\circ ,{\rm{ }}k\; \in \;\mathbb{Z}}\\{ \Leftrightarrow \;3x = 45^\circ + k180^\circ ,{\rm{ }}k\; \in \;\mathbb{Z}.}\\{ \Leftrightarrow \;x = 15^\circ + k60^\circ ,{\rm{ }}k\; \in \;\mathbb{Z}}\end{array}\)
Vậy tập nghiệm của phương trình là: \(S = \{ 15^\circ + k60^\circ ,{\rm{ }}k\; \in \;\mathbb{Z}\} .\)

a) cos3x = \(cos\left(\pi-x-\dfrac{\pi}{3}\right)\)
<=> cos3x = \(cos\left(\dfrac{2\pi}{3}-x\right)\)
<=> 3x = \(\dfrac{2\pi}{3}-x\) hoặc 3x = \(\dfrac{-2\pi}{3}+x\)
<=> 4x = \(\dfrac{2\pi}{3}+k2\pi\) hoặc 2x = \(\dfrac{-2\pi}{3}+k2\pi\)
<=> x = \(\dfrac{\pi}{6}+\dfrac{k\pi}{2}\) hoặc x = \(\dfrac{-\pi}{3}+k\pi\)
<=> x = \(\left\{\dfrac{\pi}{6}+\dfrac{k\pi}{2};\dfrac{-\pi}{3}+k\pi;k\in Z\right\}\)
b ) Điều kiện sinx\(\ne0;cosx\ne0\)
<=> sin2x\(\ne0\) <=> x \(\ne\dfrac{k\pi}{2}\);k\(\in Z\)
tanx + cotx =0
<=> tan2x + tanx =0
<=> tanx(tanx+1)=0
<=> tanx=0 hoặc tanx = -1
<=> x=\(k\pi\) (loại) hoặc x = \(\dfrac{-\pi}{4}+k\pi\)
Vậy x = \(\dfrac{-\pi}{4}+k\pi;k\in Z\)

ĐKXĐ: \(x\ne k\dfrac{\pi}{2}\)
\(tanx+\dfrac{1}{tanx}=2\)
\(\Rightarrow tan^2x+1=2tanx\)
\(\Leftrightarrow\left(tanx-1\right)^2=0\)
\(\Leftrightarrow tanx=1\)
\(\Rightarrow x=\dfrac{\pi}{4}+k\pi\) (thỏa mãn)

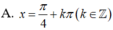
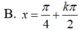

cot x = 1 ⇔ cot x = cot π/4 ⇔ x = π/4 + kπ, k ∈ Z