Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hướng dẫn làm bài:
a) Giải phương trình: x2 – x – 2 = 0
∆ = (-1)2 – 4.1.(-2) = 1 + 8 > 0
√∆ = √9 = 3
⇒ x1 = -1; x2 = 2
b) Vẽ đồ thị hàm số
- Hàm số y = x2
+ Bảng giá trị:
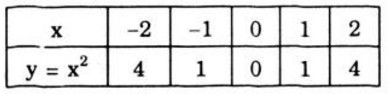
- Hàm số y = x + 2
+ Cho x = 0 ⇒ y = 2 được điểm A(0,2)
+ Cho x = -2 ⇒ y = 0 được điểm B(-2;0)
Đồ thị hàm số:

c) Ta có phương trình hoành độ giao điểm của hai đồ thị là:
x2=x+2⇔x2−x−2=0⇔{x1=−1x2=2x2=x+2⇔x2−x−2=0⇔{x1=−1x2=2
Điều này chứng tỏ rằng đồ thị đường thẳng cắt đồ thị parapol tại hai điểm có hoành độ lần lượt là x = -1; x= 2. Hai giá trị này cũng chính là nghiệm của phương trình x2 - x - 2 = 0 ở câu a).

b/ Tọa độ điểm A
\(\hept{\begin{cases}y=-x+1\\y=x+1\end{cases}}\Leftrightarrow\hept{\begin{cases}x=0\\y=1\end{cases}}\)
=> A(0, 1)
Tọa độ điểm B
\(\hept{\begin{cases}y=-x+1\\y=-1\end{cases}}\Leftrightarrow\hept{\begin{cases}x=2\\y=-1\end{cases}}\)
=> B(2, - 1)
Tọa độ điểm C
\(\hept{\begin{cases}y=x+1\\y=-1\end{cases}}\Leftrightarrow\hept{\begin{cases}x=-2\\y=-1\end{cases}}\)
=> C(-2, -1)
c/ Ta có vecto AB = (2, - 2) => AB = \(2\sqrt{2}\)
Vecto BC = (- 4, 0) => BC = 4
Vecto CA = (- 2, - 2) => CA = \(2\sqrt{2}\)
Từ đây ta có CA = AB
BC2 - AB2 - CA2 = 16 - 8 - 8 = 0
=> ∆ABC vuông cân tại A

Ta có phương trình \(\Leftrightarrow x^2y^2+y^2z^2+z^2x^2=3xyz\ge0\)
Ta lại có \(x^2y^2+y^2z^2+z^2x^2\ge3\sqrt[3]{\left(xyz\right)^4}=3xyz\sqrt[3]{xyz}\)
\(\Rightarrow3xyz\ge3xyz\sqrt[3]{xyz}\)
\(\Leftrightarrow1\ge\sqrt[3]{xyz}\ge0\)
\(\Leftrightarrow1\ge xyz>0\)
Vì x,y,z nguyên
=> xyz=1
Vậy x,y,z là \(\left\{1,1,1;1,-1,-1;-1,-1,1;-1,1,-1\right\}\)
Cre: @tpokemont

Đkxđ: \(\hept{\begin{cases}x\ge-\frac{1}{4}\\y\ge2\end{cases}}\)
\(\Leftrightarrow2+\sqrt{\left(\sqrt{x+\frac{1}{4}}+\frac{1}{2}\right)^2}=y\Leftrightarrow2+\frac{1}{2}+\sqrt{x+\frac{1}{2}}=y\Leftrightarrow\sqrt{x+\frac{1}{2}}+\frac{5}{2}=y\)
do x,y nguyên dương nên \(\sqrt{x+\frac{1}{2}}+\frac{5}{2}\)nguyên dương\(\Leftrightarrow\sqrt{x+\frac{1}{2}}=\frac{k}{2}\)(K là số nguyên lẻ, \(k>1\))
\(\Rightarrow x=\frac{k^2-2}{4}\)
do \(k^2\)là số chính phương chia 4 dư 0,1 \(\Rightarrow x=\frac{k^2-2}{4}\notin Z\)
=> ko tồn tại cặp số nguyên dương x,y tmđkđb
ta có: \(x-\frac{91}{y}=2\)
<=> \(xy-91=2y\) ( với \(y\ne0\))
<=>\(y\left(x-2\right)=91\)
đến đây tự giải đc rồi nha!