
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


TH1: \(m=-1\) thỏa mãn (dễ dàng kiểm tra các giá trị \(f\left(-1\right)>0\) ; \(f\left(0\right)< 0\) ; \(f\left(3\right)>0\) nên pt có ít nhất 2 nghiệm thuộc (-1;0) và (0;3)
TH2: \(m>-1\):
\(\lim\limits_{x\rightarrow+\infty}f\left(x\right)=\lim\limits_{x\rightarrow+\infty}x^4\left[m\left(1-\dfrac{2}{x}\right)^2\left(1+\dfrac{9}{x}\right)+1-\dfrac{32}{x^4}\right]=+\infty.\left(m+1\right)=+\infty>0\)
\(\Rightarrow\) Luôn tồn tại 1 giá trị \(x=a\) đủ lớn sao cho \(f\left(a\right)>0\)
\(f\left(0\right)=-32< 0\Rightarrow f\left(a\right).f\left(0\right)< 0\)
\(\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm dương
\(f\left(-9\right)=9^4-32>0\Rightarrow f\left(-9\right).f\left(0\right)< 0\)
\(\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm âm thuộc \(\left(-9;0\right)\)
\(\Rightarrow f\left(x\right)\) luôn có ít nhất 2 nghiệm
TH3: \(m< -1\) tương tự ta có: \(\lim\limits_{x\rightarrow+\infty}f\left(x\right)=\lim\limits_{x\rightarrow-\infty}=+\infty.\left(m+1\right)=-\infty\)
\(\Rightarrow\) Luôn tồn tại 1 giá trị \(x=a>0\) đủ lớn và \(x=b< 0\) đủ nhỏ sao cho \(\left\{{}\begin{matrix}f\left(a\right)< 0\\f\left(b\right)< 0\end{matrix}\right.\)
Lại có \(f\left(-9\right)=9^4-32>0\) \(\Rightarrow\left\{{}\begin{matrix}f\left(-9\right).f\left(a\right)< 0\\f\left(-9\right).f\left(b\right)< 0\end{matrix}\right.\)
\(\Rightarrow\) Pt luôn có ít nhất 2 nghiệm thuộc \(\left(-\infty;-9\right)\) và \(\left(-9;+\infty\right)\)
Vậy pt luôn có ít nhất 2 nghiệm với mọi m

điều kiện xác định \(\left\{{}\begin{matrix}cos\left(3x-\dfrac{\pi}{2}\right)\ne0\\sinx\ne0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}3x-\dfrac{\pi}{2}\ne\dfrac{\pi}{2}+k2\pi\\x\ne k\pi\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ne\dfrac{\pi}{3}+\dfrac{2}{3}k\pi\\x\ne k\pi\end{matrix}\right.\) \(\left(k\in Z\right)\)
ta có : \(tan\left(3x-\dfrac{\pi}{2}\right)+cotx=0\)
\(\Leftrightarrow tan\left(3x-\dfrac{\pi}{2}\right)+cot\left(\dfrac{\pi}{2}-\left(\dfrac{\pi}{2}-x\right)\right)=0\)
\(\Leftrightarrow tan\left(3x-\dfrac{\pi}{2}\right)-tan\left(\dfrac{\pi}{2}-x\right)=0\)
\(\Leftrightarrow tan\left(3x-\dfrac{\pi}{2}\right)=tan\left(\dfrac{\pi}{2}-x\right)\) \(\Leftrightarrow3x-\dfrac{\pi}{2}=\dfrac{\pi}{2}-x+k\pi\Leftrightarrow4x=\pi+k\pi\)
\(\Leftrightarrow x=\dfrac{\pi}{4}+\dfrac{k\pi}{4}\left(k\in Z\right)\left(tmđk\right)\)
vậy phương trình có một hệ nghiệm duy nhất là \(x=\dfrac{\pi}{4}+\dfrac{k\pi}{4}\)

Áp dụng công thức \(\left(\dfrac{1}{v}\right)'=\dfrac{-v'}{v^2}\)
Ta có \(y'=\dfrac{-\left(x^2+x-1\right)'}{\left(x^2+x-1\right)^2}=-\dfrac{\left(2x+1\right)}{\left(x^2+x-1\right)^2}\)


a. vs m + 2
=>pttt : cos3x.cosx-sin2x+sin3xsinx+1=0
<=>\(\dfrac{1}{2}\left(cos2x+cos4x+cos2x-cos4x\right)-sin2x+1\)=0
<=>\(\dfrac{1}{2}\).2cos2x-sin2x+1=0
<=>cos2x-sin2x+1=0
<=>cos2x-sin2x-2sinxcosx+1=0
<=>cos2x+cos2x-sin2x=0
<=>2cos2x-2sinxcosx=0
<=>2cosx(cosx-sinx)=0
<=>\(\left[{}\begin{matrix}2cosx=0\\cosx-sinx=0\end{matrix}\right.\)
<=>\(\left[{}\begin{matrix}x=\dfrac{\pi}{2}+k\pi\\x=\dfrac{\pi}{4+k\pi}\end{matrix}\right.\)(k thuộc Z)

Mình vội nên suy nghĩ có 5 phút nếu sai sót gì mong bạn thông cảm
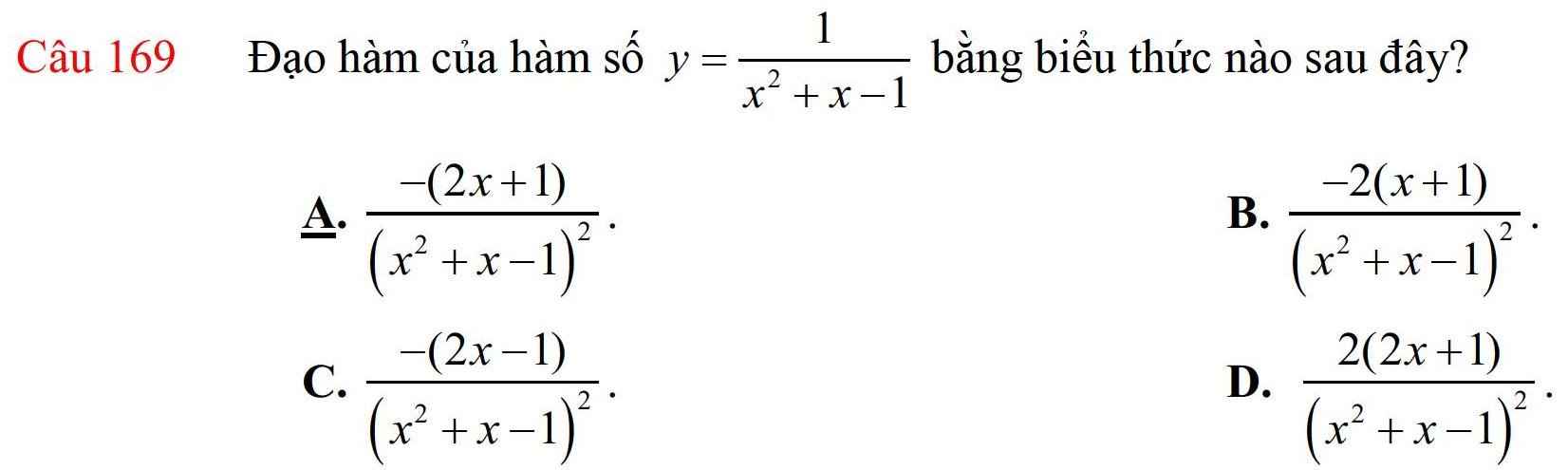

2cos8x-8coos4x+5=0
<=>2(2cos24x-1)-8cos4x+5=0
<=>4cos24x-8cos4x+3=0
<=>cos4x=\(\dfrac{1}{2}\) <=> 4x=\(\dfrac{\pi}{3}+k2\pi\) hoặc 4x=\(\dfrac{-\pi}{3}+k2\pi\)
<=>x=\(\dfrac{\pi}{12}+\dfrac{k\pi}{2}\) hoặc x=\(\dfrac{-\pi}{12}+\dfrac{k\pi}{2}\)