
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


`#3107.101107`
`A = 1+ 3 + 3^2+3^3+…+3^101?`
`= (1 + 3 + 3^2) + (3^3 + 3^4 + 3^5) + ... + (3^99 + 3^100 + 3^101)`
`= (1 + 3 + 3^2) + 3^3 * (1 + 3 + 3^2) + ... + 3^99 * (1 + 3 + 3^2)`
`= (1 + 3 + 3^2) * (1 + 3^3 + ... + 3^99)`
`= 13 * (1 + 3^3 + ... + 3^99)`
Vì `13 * (1 + 3^3 + ... + 3^99) \vdots 13`
`=> A \vdots 13`
Vậy, `A \vdots 13.`

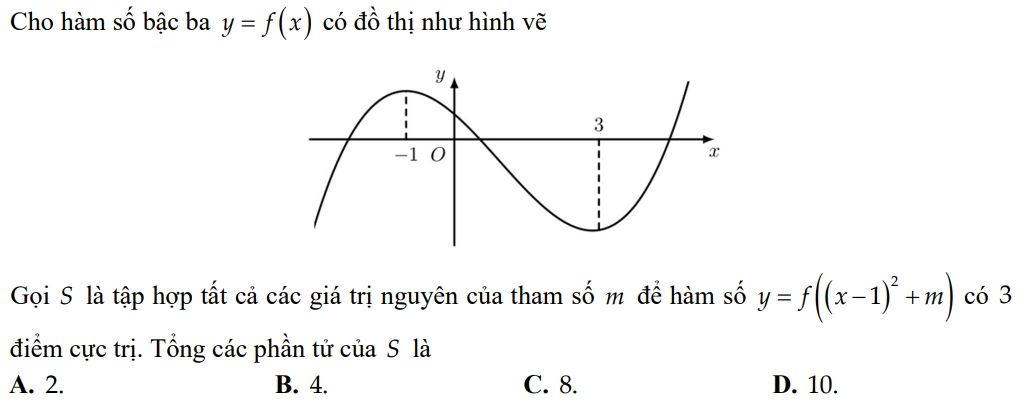
Bài này làm khá tắt chỗ 3 điểm cực trị, mình trình bày lại để bạn dễ hiểu nhé!
.......
Để y' = 0\(\Leftrightarrow\left[{}\begin{matrix}x=1\\f'\left(\left(x-1\right)^2+m\right)=0\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=1\\\left(x-1\right)^2+m=-1\\\left(x-1\right)^2+m=3\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=1\\\left(x-1\right)^2=-1-m\left(1\right)\\\left(x-1\right)^2=3-m\left(2\right)\end{matrix}\right.\)
Để hàm số có 3 điểm cực trị thì y' = 0 có 3 nghiệm phân biệt.
Ta có 2 trường hợp.
+) \(TH_1:\) (1) có nghiệm kép x = 1 hoặc vô nghiệm và (2) có hai nghiệm phân biệt khác 1.
\(\Rightarrow\left[{}\begin{matrix}-1-m\le0\\3-m>0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}m\ge-1\\m< 3\end{matrix}\right.\) \(\Leftrightarrow-1\le m< 3\)
+) \(TH_2:\) (2) có nghiệm kép x = 1 và (2) có một nghiệm phân biệt khác 1.
\(\Rightarrow\left[{}\begin{matrix}-1-m>0\\3-m\le0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}m< -1\\m\ge3\end{matrix}\right.\) \(\Leftrightarrow m\in\varnothing\)
\(\Rightarrow-1\le m< 3\Rightarrow S=\left\{-1;0;1;2\right\}\)
Do đó tổng các phần tử của S là \(-1+0+1+2=2\)

\(y'=4x^3-4x=0\Rightarrow\left[{}\begin{matrix}x=0\Rightarrow y=1\\x=1\Rightarrow y=0\\x=-1\Rightarrow y=0\end{matrix}\right.\)
\(\Rightarrow A\left(0;1\right);B\left(1;0\right);C\left(-1;0\right)\)
\(S=\dfrac{1}{2}.\left|y_A-y_B\right|.\left|x_B-x_C\right|=\dfrac{1}{2}.1.2=1\)

B, Đồ thị y thì nhìn vào dáng điệu, đồ thị y' thì chú ý trục hoành


Câu 12:
Để hàm số $y$ đồng biến trên từng khoảng xác định thì:
\(y'=\frac{m+1}{(x+1)^2}> 0, \forall x\in (-\infty;-1)\cup (-1;+\infty)\)
\(\Leftrightarrow m> -1\)
Đáp án B.
Câu 13:
$y=x^3-3m^2x$
$y'=3x^2-3m^2$. Để $y$ đồng biến trên $\mathbb{R}$ thì $y'\geq 0, \forall x\in\mathbb{R}$
$\Leftrightarrow x^2\geq m^2, \forall x\in\mathbb{R}$
$\Leftrightarrow m^2\leq min (x^2)=0$. Điều này xảy ra khi $m=0$
Đáp án D.

txđ D=R
y'=-3x2+6x+3m
y' là tam thức bậc 2 nên y'=0 có tối đa 2 nghiệm
để hs nb/(0;\(+\infty\) ) thì y' \(\le\) 0 với mọi x \(\in\) (0;\(+\infty\) )
\(\Leftrightarrow\) -3x2 +6x+3m \(\le\) 0 với mọi x \(\in\) (0;\(+\infty\) )
\(\Leftrightarrow\) m\(\le\) x2 -2x với mọi x \(\in\) (0; \(+\infty\) )
xét hs g(x)=x2 -2x
g'(X) =2x-2
g'(x)=0 \(\Leftrightarrow\) x=1
vậy m \(\le\) -1









Lời giải:
a) Đặt \(\left\{\begin{matrix} u=x\\ dv=\cos 2xdx\end{matrix}\right.\Rightarrow \left\{\begin{matrix} du=dx\\ v=\frac{\sin 2x}{2}\end{matrix}\right.\)
\(\Rightarrow \int x\cos 2xdx=\frac{x\sin 2x}{2}-\int \frac{\sin 2x}{2}dx=\frac{x\sin 2x}{2}+\frac{\cos 2x}{4}\)
\(\Rightarrow \int ^{\frac{\pi}{2}}_{0}x\cos 2xdx=\left.\begin{matrix} \frac{\pi}{2}\\ 0\end{matrix}\right|\left ( \frac{x\sin 2x}{2}+\frac{\cos 2x}{4} \right )=\frac{-1}{2}\)
b) Đặt \(\left\{\begin{matrix} u=x\\ dv=e^{-2x}dx\end{matrix}\right.\Rightarrow \left\{\begin{matrix} du=dx\\ v=\frac{-e^{-2x}}{2}\end{matrix}\right.\)
\(\Rightarrow \int xe^{-2x}dx=\frac{-xe^{-2x}}{2}+\int \frac{e^{-2x}}{2}dx=\frac{-xe^{-2x}}{2}-\frac{e^{-2x}}{4}\)
\(\Rightarrow \int ^{\ln 2}_{0}xe^{-2x}dx=\left.\begin{matrix} \ln 2\\ 0\end{matrix}\right|\left ( \frac{-xe^{-2x}}{2}-\frac{e^{2x}}{4} \right )=\frac{3}{16}-\frac{\ln 2}{8}\)
c)
\(\int ^{1}_{0}\ln (2x+1)dx=\frac{1}{2}\int ^{1}_{0}\ln (2x+1)d(2x+1)=\frac{1}{2}\int ^{3}_{1}\ln tdt\)
Đặt \(\left\{\begin{matrix} u=\ln t\\ dv=dt\end{matrix}\right.\Rightarrow \left\{\begin{matrix} du=\frac{dt}{t}\\ v=t\end{matrix}\right.\Rightarrow \int \ln tdt=t\ln t-\int dt=t\ln t-t\)
Do đó \(\frac{1}{2}\int ^{3}_{1}\ln tdt=\left.\begin{matrix} 3\\ 1\end{matrix}\right|\left(\frac{t\ln t-t}{2}\right)=\frac{3\ln 3}{2}-1\)
d)
Ta có \(\int ^{3}_{2}(\ln (x-1)-\ln (x+1))dx=\int ^{3}_{2}\ln (x-1)d(x-1)-\int ^{3}_{2}\ln (x+1)d(x+1)\)
\(=\int ^{2}_{1}\ln tdt-\int ^{4}_{3}\ln tdt\)
Theo phần c, ta đã chỉ ra được \(\int \ln tdt=t\ln t-t\), do đó:
\(\int ^{2}_{1}\ln tdt-\int ^{4}_{3}\ln tdt=\left.\begin{matrix} 2\\ 1\end{matrix}\right|(t\ln t-t)-\left.\begin{matrix} 4\\ 3\end{matrix}\right|(t\ln t-t)=\ln \left(\frac{27}{64}\right)\)
e)
Xét \(\int (x+1-\frac{1}{x})e^{x+\frac{1}{x}}dx=\int e^{x+\frac{1}{x}}dx+\int \left (x-\frac{1}{x}\right)e^{x+\frac{1}{x}}dx\)
Đặt \(\left\{\begin{matrix} u=e^{x+\frac{1}{x}}\\ dv=dx\end{matrix}\right.\Rightarrow \left\{\begin{matrix} du=\left(1-\frac{1}{x^2}\right)e^{x+\frac{1}{x}}dx\\ v=x\end{matrix}\right.\)
\(\Rightarrow \int e^{x+\frac{1}{x}}dx=xe^{x+\frac{1}{x}}-\int \left(x-\frac{1}{x}\right)e^{x+\frac{1}{x}}dx\)
Do đó \(\int \left(x+1-\frac{1}{x}\right)e^{x+\frac{1}{x}}dx=xe^{x+\frac{1}{x}}\)
\(\int ^{2}_{\frac{1}{2}}\left(x+1-\frac{x}{x}\right)e^{x+\frac{1}{x}}dx=\left.\begin{matrix} 2\\ \frac{1}{2}\end{matrix}\right|xe^{x+\frac{1}{x}}=\frac{3e^{\frac{5}{2}}}{2}\)