Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



1) Ta có pt \(\Leftrightarrow\sqrt{x+1}+2x\sqrt{x+3}=2x+\sqrt{\left(x+1\right)\left(x+3\right)}\)
Đặt \(\sqrt{x+1}=a;\sqrt{x+3}=b\left(b>a\ge0\right)\)
Ta có pt \(\Leftrightarrow a+2xb=2x+ab\Leftrightarrow a\left(1-b\right)-2x\left(1-b\right)=0\Leftrightarrow\left(a-2x\right)\left(1-b\right)=0\)
Đến đây tự thay a,b vào rồi giải pt bậc 2 nhá !
b, trừ từng vế của 2 pt trong hệ ta có pt hệ quả có nhân tử chung là x-y

\(\Leftrightarrow\hept{\begin{cases}y=5-2x\\5x+2.\left(5-2x\right)=12\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}y=5-2x\\5x+10-4x=12\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}y=5-2x\\x=12-10\end{cases}\Leftrightarrow\hept{\begin{cases}y=5-2.2=1\\x=2\end{cases}}}\)

Đây là hệ phương trình Đồng bậc rồi. Chỉ cần nhân chéo là OK thôi.
Lời giải:
ĐK: \(x,y\ne0\)
Ta có: \(\hept{\begin{cases}x=\frac{x^2+12}{2y^2}\\y=\frac{y^2+12}{2x^2}\end{cases}}\Leftrightarrow\hept{\begin{cases}x^2+12=2xy^2\\y^2+12=2x^2y\end{cases}}\) (thực hiện nhân chéo)
Trừ theo vế: \(\Rightarrow x^2-y^2=2xy^2-2x^2y\)
\(\Leftrightarrow\left(x-y\right)\left(x+y\right)=2xy\left(y-x\right)\)
\(\Leftrightarrow\left(x-y\right)\left(x+y\right)+2xy\left(x-y\right)=0\)
\(\Leftrightarrow\left(x-y\right)\left(x+y+2xy\right)=0\)
Do \(x=\frac{x^2+12}{2y^2}\) có \(x^2,y^2>0\Rightarrow x>0\), tương tự thì \(y>0\). Do đó \(x+y+2xy>0\)
\(\Rightarrow x-y=0\Leftrightarrow x=y\)
Thay vào phương trình đầu tiên: \(x=\frac{x^2+12}{2x^2}\Rightarrow2x^3=x^2+12\)
\(\Leftrightarrow\left(x-2\right)\left(2x^2+3x+6\right)=0\)
Thấy rằng \(2x^2+3x+6=x^2+\left(x+\frac{3}{2}\right)^2+\frac{15}{4}>0\Rightarrow x=2\rightarrow y=2\)
Vậy hpt có nghiệm \(\left(x,y\right)=\left(2,2\right)\)

Cách 1
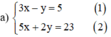
Từ (1) ta rút ra được y = 3x – 5 (*)
Thế (*) vào phương trình (2) ta được :
5x + 2(3x – 5) = 23 ⇔ 5x + 6x – 10 = 23 ⇔ 11x = 33 ⇔ x = 3.
Thay x = 3 vào (*) ta được y = 3.3 – 5 = 4.
Vậy hệ phương trình có nghiệm duy nhất (3 ; 4).