
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(f'\left(x\right)=-3x^2+m\)
TH1: \(m\le0\Rightarrow f\left(x\right)\) nghịch biến trên R
\(\Rightarrow\max\limits_{\left[1;3\right]}f\left(x\right)=f\left(1\right)=m-7=10\Rightarrow m=17>0\left(ktm\right)\)
TH2: \(m>0\Rightarrow\) hàm có 2 điểm cực trị \(x=\pm\sqrt{\dfrac{m}{3}}\) \(\Rightarrow\) hàm nghịch biến trên \(\left(\dfrac{\sqrt{m}}{3};+\infty\right)\) và đồng biến trên \(\left(-\sqrt{\dfrac{m}{3}};\sqrt{\dfrac{m}{3}}\right)\)
- Nếu \(\sqrt{\dfrac{m}{3}}\ge3\Rightarrow m\ge27\Rightarrow\) hàm đồng biến trên \(\left[1;3\right]\)
\(\Rightarrow\max\limits_{\left[1;3\right]}f\left(x\right)=f\left(3\right)=3m-33=10\Rightarrow m=\dfrac{40}{3}< 27\left(ktm\right)\)
- Nếu \(\sqrt{\dfrac{m}{3}}\le1\Rightarrow m\le3\Rightarrow\) hàm nghịch biến trên \(\left[1;3\right]\)
\(\Rightarrow\max\limits_{\left[1;3\right]}f\left(x\right)=f\left(1\right)=m-7=10\Rightarrow m=17>3\left(ktm\right)\)
- Nếu \(1< \sqrt{\dfrac{m}{3}}< 3\Rightarrow3< m< 27\) \(\Rightarrow x=\sqrt{\dfrac{m}{3}}\) là điểm cực đại và là cực trị duy nhất thuộc \(\left[1;3\right]\)
\(\Rightarrow\max\limits_{\left[1;3\right]}f\left(x\right)=f\left(\sqrt{\dfrac{m}{3}}\right)=-\dfrac{m}{3}\sqrt{\dfrac{m}{3}}+m\sqrt{\dfrac{m}{3}}-6=10\)
\(\Rightarrow m=12\) (thỏa mãn)
\(\Rightarrow m-x_0=12-\sqrt{\dfrac{12}{3}}=10\)

ĐKXĐ: \(x>0\)
Đặt \(\log_\frac{22}{3}x=t\) BPT trở thành:
\(\sqrt{2t^2-2t+5}-\sqrt{13}+\sqrt{2t^2-4t+4}\le0\)
\(\Leftrightarrow\sqrt{4t^2-4t+10}+\sqrt{4t^2-8t+8}\le\sqrt{26}\)
\(\Leftrightarrow\sqrt{\left(2t-1\right)^2+9}+\sqrt{\left(2-2t\right)^2+4}\le\sqrt{26}\) (1)
Ta có:
\(\sqrt{\left(2t-1\right)^2+3^2}+\sqrt{\left(2-2t\right)^2+2^2}\ge\sqrt{\left(2t-1+2-2t\right)+\left(3+2\right)^2}=\sqrt{26}\) (2)
(1);(2) \(\Rightarrow\sqrt{\left(2t-1\right)^2+9}+\sqrt{\left(2t-2\right)^2+4}=\sqrt{26}\)
Đẳng thức xảy ra khi và chỉ khi:
\(\dfrac{2t-1}{2-2t}=\dfrac{3}{2}\Rightarrow t=\dfrac{4}{5}\)
\(\Rightarrow \log_\frac{22}{3}x=\dfrac{4}{5}\)
\(\Rightarrow x=\left( \dfrac{22}{3}\right)^\frac{4}{5}\) \(\approx4,923\)
D là đáp án đúng


\(2^x-6^x-3^{x+1}+3=0\)
\(\Leftrightarrow2^x\left(1-3^x\right)+3\left(1-3^x\right)=0\)
\(\Leftrightarrow\left(2^x+3\right)\left(1-3^x\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2^x+3=0\left(\text{vô nghiệm}\right)\\1-3^x=0\end{matrix}\right.\)
\(\Rightarrow3^x=1\Rightarrow x=0\)
Để giải phương trình , trước hết hãy viết lại phương trình theo thứ tự các thành phần của :
Kết hợp các thành phần có cùng :
Bây giờ, để tìm giá trị của , hãy giải phương trình:
Đưa hằng số về phía bên kia của phương trình:
Giải phương trình để tìm giá trị của :
Vậy giá trị của là .
Để giải phương trình , trước hết hãy viết lại phương trình theo thứ tự các thành phần của :
Kết hợp các thành phần có cùng :
Bây giờ, để tìm giá trị của , hãy giải phương trình:
Đưa hằng số về phía bên kia của phương trình:
Giải phương trình để tìm giá trị của :
Vậy giá trị của là .

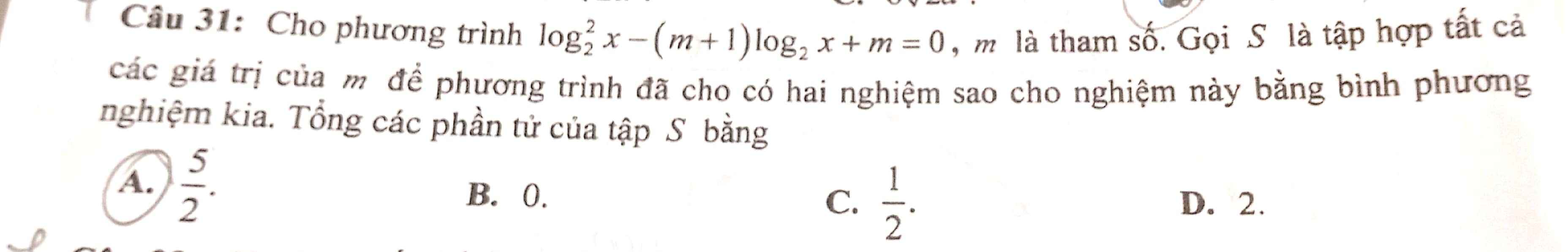

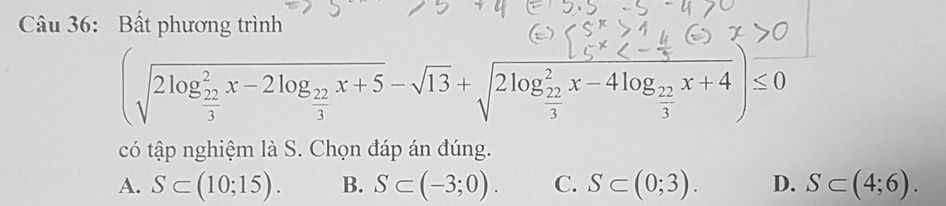
 giải giúp e câu 2,4,5,6 vs ạ.
giải giúp e câu 2,4,5,6 vs ạ.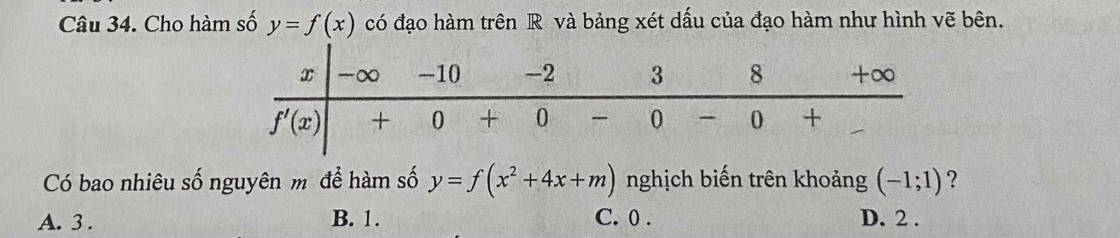



ĐKXĐ: \(x>0\)
\(log_2^2x-m.log_2x-log_2x+m=0\)
\(\Leftrightarrow log_2x\left(log_2x-m\right)-\left(log_2x-m\right)=0\)
\(\Leftrightarrow\left(log_2x-1\right)\left(log_2x-m\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x_1=2\\x_2=2^m\end{matrix}\right.\)
TH1: \(x_1=x_2^2\Leftrightarrow2=\left(2^m\right)^2=2^{2m}\Rightarrow2m=1\Rightarrow m=\dfrac{1}{2}\)
TH2: \(x_2=x_1^2\Rightarrow2^m=2^2\Rightarrow m=2\)
\(\Rightarrow2+\dfrac{1}{2}=\dfrac{5}{2}\)