
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


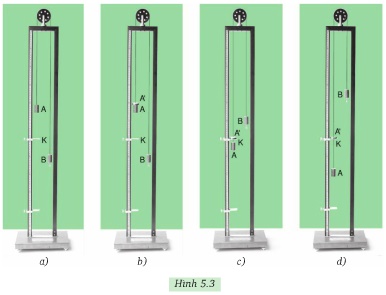
Quả cân A chịu tác dụng của hai lực : Trọng lực và sức căng
của dây, hai lực này cân bằng (do T = PB mà PB = PA nên
cân bằng với
.
Quả cầu A ban đầu đứng yên là do trọng lực tác dụng lên A và lực căng dây cân bằng với nhau. Lực căng này cũng cân bằng với trọng lực tác dụng lên B.


a) \(\overrightarrow{F_1}\) : tại điểm đặt A, phương thẳng đứng, chiều từ dưới lên, cường độ lực F1 = 20N.
b) \(\overrightarrow{F_2}\) : điểm đặt tại B, phương nằm ngang, chiều từ trái sang phải, cường độ F2 = 30N.
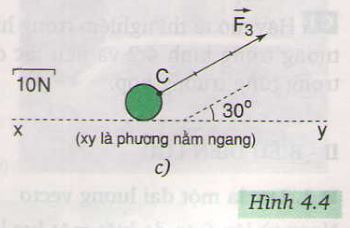
c) \(\overrightarrow{F_3}\) : điểm đặt tại C, phương nghiêng một góc 30o so với phương nằm ngang, chiều hướng lên, cường độ F3 = 30N
\(\overrightarrow{F_1}\):Điểm đặt tại A,phương thẳng đứng,chiều từ dưới lên trên,độ lớn F1=20N
\(\overrightarrow{F_2}\):Điểm đặt tại B,phương nằm ngang,chiều từ trái sang phải,độ lớn F2=30N
\(\overrightarrow{F_3}\):Điểm đặt tại C,phương nằm nghiêng 1 góc 300 so với phương nằm ngang,chiều từ trái sang phải,độ lớn F3=30N

Đặt thêm một vật nặng A’ lên quả cân A, lúc này PA + PA’, lớn hơn t nên vật AA’ chuyển động nhanh dần đi xuống, B chuyển động đi lên.
Đặt thêm vật nặng A' thì trọng lực tác dụng lên hệ (A+A') lớn hơn (thắng) lực căng dây vào kéo (A+A') chuyển động nhanh dần đi xuống.

Hình 4.1 : Lực hút của nam châm lên miếng thép làm tăng vận tốc của xe lăn, nên xe lăn chuyển động nhanh lên.
Hình 4.2 : Lực tác dụng của vợt nên quả bóng làm quả bóng bị biến dạng và ngược lại, lực mà quả bóng đập vào vợt làm vợt bị biến dạng.
+hình 4.1: Đưa nam châm vĩnh cửu lại gần chiếc xe đồ chơi, trên xe có đặt một thỏi sắt. Nam châm hút thỏi sắt và kéo chiếc xe chạy lại gần thỏi sắt. Lực tác dụng trong trường hợp này là lực hút giữa nam châm và thỏi sắt.
+hình 4.2: Trái banh bị cây vợt tác dụng lực vào thì bị biến dạng và bay đi (tức bị thay đổi vận tốc). Lực tác dụng trong trường hợp này là lực đẩy giữa vọt và trái banh.

Giải:
a) Lực ma sát trượt giữa đĩa và xích làm mòn đĩa xe và xích nên cần kiểm tra dầu vào xích xe để làm giảm ma sát.
b) Lực ma sát trượt của trục làm mòn trục và cản chuyển động quay của bánh xe. Muốn giảm ma sát thì thay bằng trục quay có ổ bi, khi đó lực ma sát giảm tới 20 lần, 30 lần so với lúc chưa có ổ bi.
c) Lực ma sát trượt cản trở chuyển động của thùng khi đẩy. Muốn giảm ma sát, dùng bánh xe thay thế mà sát trượt bằng ma sát lăn (nhờ đặt thùng đồ lên bàn có bánh xe).
a) Lực ma sát trượt giữa đĩa và xích làm mòn đĩa xe và xích nên cần kiểm tra dầu vào xích xe để làm giảm ma sát.
b) Lực ma sát trượt của trục làm mòn trục và cản chuyển động quay của bánh xe. Muốn giảm ma sát thì thay bằng trục quay có ổ bi, khi đó lực ma sát giảm tới 20 lần, 30 lần so với lúc chưa có ổ bi.
c) Lực ma sát trượt cản trở chuyển động của thùng khi đẩy. Muốn giảm ma sát, dùng bánh xe thay thế mà sát trượt bằng ma sát lăn (nhờ đặt thùng đồ lên bàn có bánh xe).

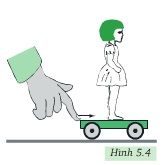
Búp bê sẽ ngã về phía trước
Vì khi xe dừng lại đột ngột, chân búp bê dừng lại theo xe nhưng do quán tính thân búp bê vẫn muốn tiếp tục chuyển động nên búp bê ngã về phía trước
búp bê sẽ ngã về phía trước. Vì khi xe dừng đột ngột, mặc dù chân búp bê đã dừng lại cùng với xe nhưng do quán tính nên thân búp bê vẫn chuyển động và nó nhào về phía trước.

ví dụ dòng nước chảy đứng yên so với thuyền hoặc bè trôi trên dòng nước

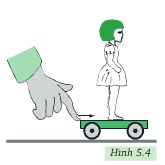
Búp bê ngã về phía sau.
Vì khi xe bất chợt chuyển động về phía trước, chân búp bê chuyển động chuyển động theo xe nhưng do quán tính thân búp bê vẫn muốn đứng yên nên búp bê ngã về phía sau
Búp bê sẽ ngã về phía bên trái vì:
Giả sử có 1 hòn đá ở phía trước cái xe. Xe chuyển động về phía trước thì thế nào xe cũng sẽ đổ về phía bên trái.
Đó là câu trả lời của em. Em mới học lớp 5 thôi ạ.





Do cục đá nổi trên mặt nước nên P = FA => dn . Vc = dv . Vv
\(\Rightarrow V_{chìm}=\dfrac{d_v.V_v}{d_n}=\dfrac{9000.4.10^{-4}}{1000.10}=\dfrac{3,6}{10000}=3,6.10^{-4}\left(m^3\right)=360\left(cm^3\right)\)