K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
3 tháng 7 2023
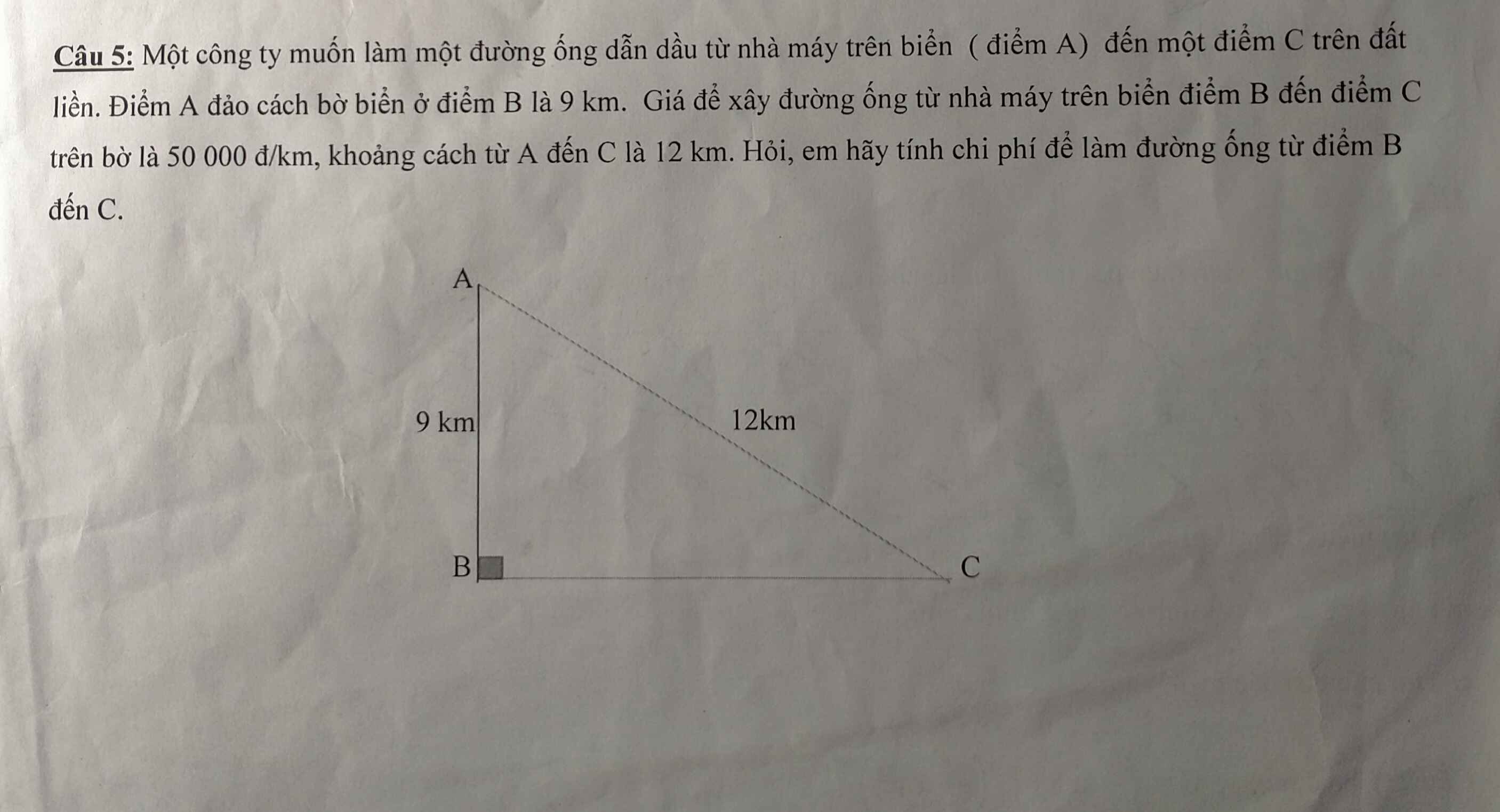
BC=căn 12^2-9^2=3căn 7(km)
Số tiền cần làm là:
3*căn 7*50000=396862,7(đồng)
26 tháng 2 2022
a: \(f\left(x\right)+g\left(x\right)=x^3-3x^2+6x-8+x^3-6x^2+12x-8\)
\(=2x^3-9x^2+18x-16\)
b: \(f\left(1\right)=1^3-3\cdot1^2+6\cdot1-8=1-3+6-8=-2+6-8=4-8=-4\)
\(g\left(-1\right)=-6\cdot\left(-1\right)^2+\left(-1\right)^3-8+12\cdot\left(-1\right)\)
\(=-6\cdot1-1-8-12\)
=-6-21
=-27
c: f(x)-g(x)=0
=>f(x)=g(x)
\(\Leftrightarrow x^3-3x^2+6x-8=x^3-6x^2+12x-8\)
\(\Leftrightarrow3x^2-6x=0\)
=>3x(x-2)=0
=>x=0 hoặc x=2
26 tháng 2 2022
Bài 7:
Đặt f(x)=a; g(x)=b
Theo đề, ta có: \(\left\{{}\begin{matrix}a+b=5x^2-2x+3\\a-b=x^2-2x+5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2a=6x^2-4x+8\\a-b=x^2-2x+5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}f\left(x\right)=3x^2-2x+4\\g\left(x\right)=3x^2-2x+4-x^2+2x-5=2x^2-1\end{matrix}\right.\)
14 tháng 4 2021
Gọi gốc là điểm A, chỗ gãy là B, ngọn đã gãy là điểm C
Xét tam giác ABC vuông tại A có: AB = 6m, BC = 16m - 6m = 10m
=> AB2 + AC2 = BC2 (Định lý Py-ta-go)
Thay: 62 + AC2 = 102
36 + AC2 = 100
AC2 = 100 - 36 = 64
AC = 8 (m)
Vậy khoảng cách từ gốc đến ngọn cây bị gãy là 8 mét
Nếu đúng hãy K cho mình nha
Học tốt nhé
13 tháng 4 2021
Bài 6:
a) Xét ΔABH vuông tại H và ΔACH vuông tại H có
AB=AC(ΔABC cân tại A)
AH chung
Do đó: ΔABH=ΔACH(cạnh huyền-cạnh góc vuông)
LH
2
10 tháng 10 2021
\(\left(4x-1\right)^3=-\dfrac{1}{27}\)
\(\Rightarrow4x-1=-\dfrac{1}{3}\)
\(\Rightarrow4x=\dfrac{2}{3}\Rightarrow x=\dfrac{1}{6}\)
10 tháng 10 2021
\(\left(4x-1\right)^3=\left(-\dfrac{1}{27}\right)\Leftrightarrow4x-1=-\dfrac{1}{3}\Leftrightarrow4x=\dfrac{2}{3}\Leftrightarrow x=\dfrac{1}{6}\)
2D
1
15 tháng 10 2021
Bài 2:
Áp dụng tính chất của dãy tỉ số bằng nhau,ta được
\(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{4}=\dfrac{a+b+c}{2+3+4}=\dfrac{45}{9}=5\)
Do đó: a=10; b=15;c=20
Q
1
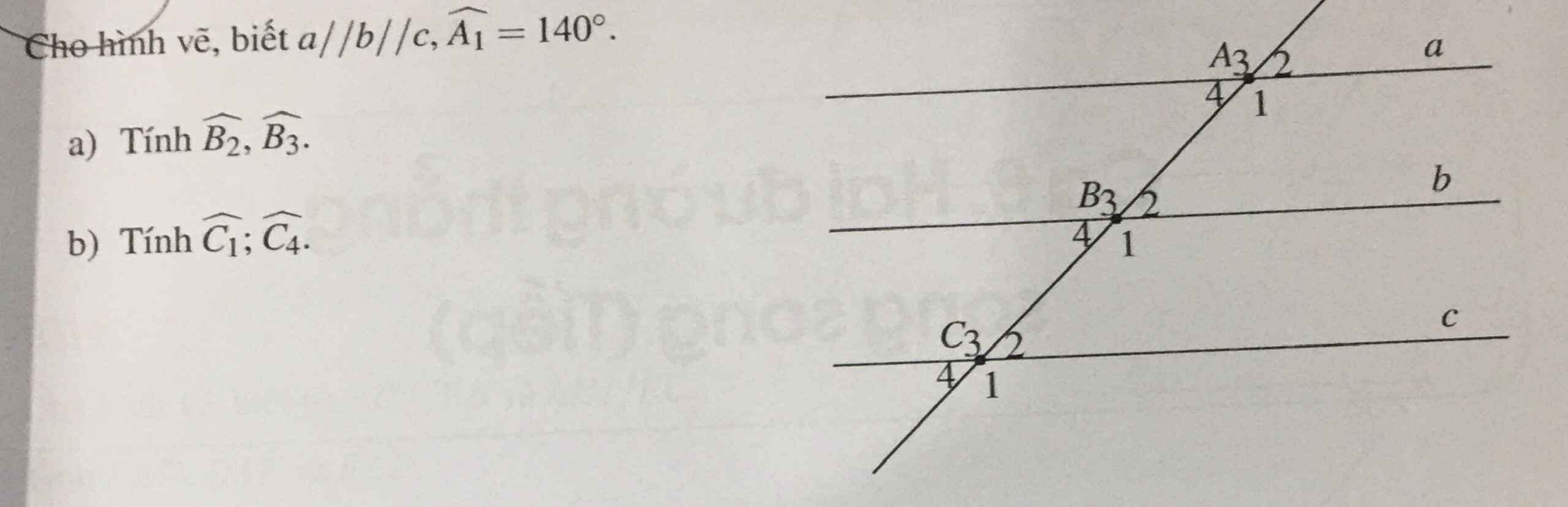
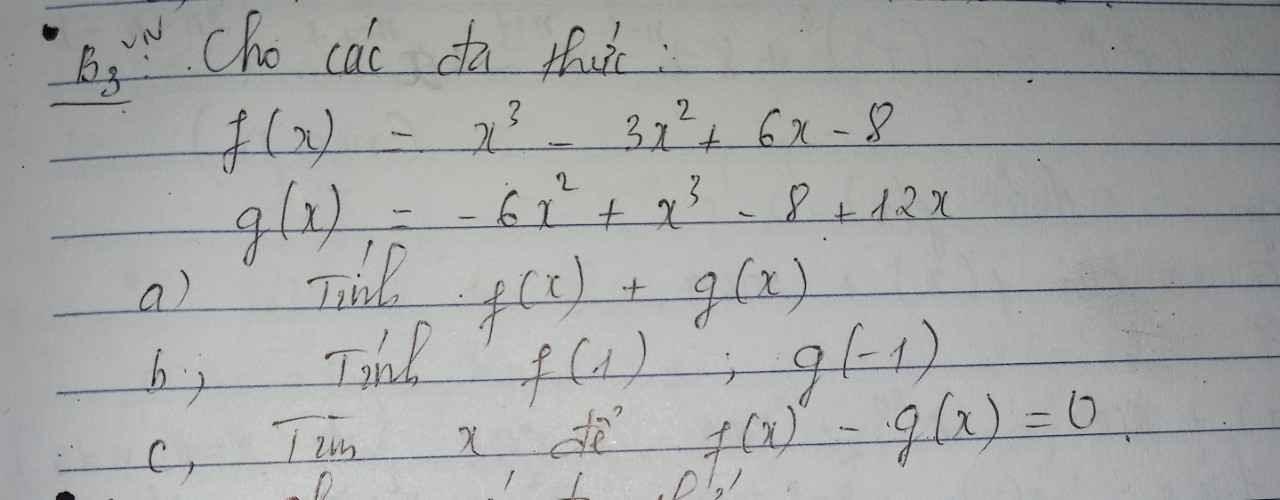
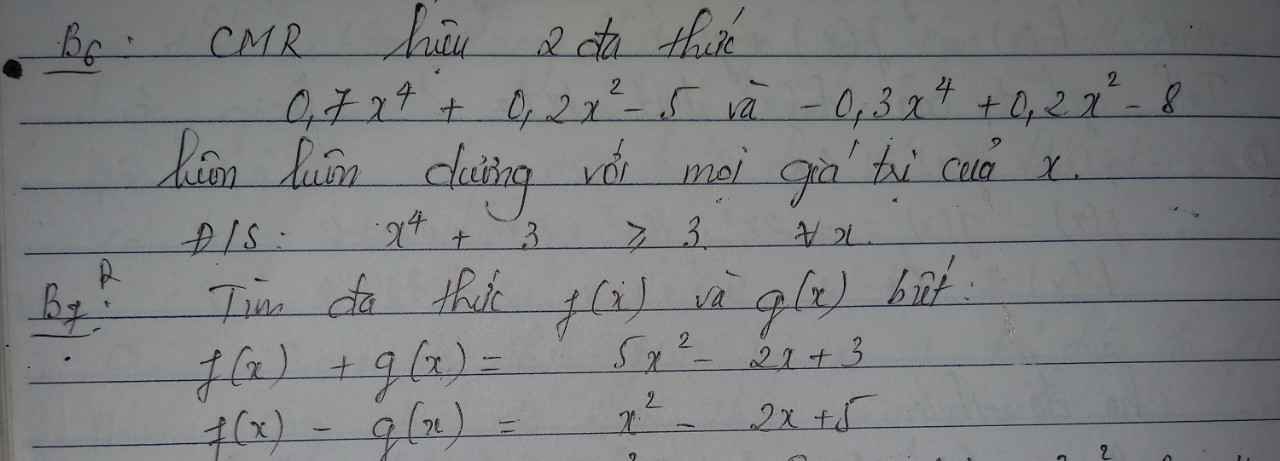
\(a//b//c\)
\(=>\angle\left(A1\right)+\angle\left(B2\right)=180^o\)(2 góc ở vị trí trong cùng phía)
\(=>\angle\left(B2\right)=180^0-140^0=40^o\)
có \(\angle\left(B3\right)+\angle\left(B2\right)=180^o\left(ke-bu\right)\)
\(=>\angle\left(B3\right)=180^0-40^0=140^o\)
b, \(\angle\left(B2\right)+\angle\left(B1\right)=180^o\left(ke-bu\right)\)
\(=>\angle\left(B1\right)=180^o-40^o=140^o\)
\(b//c=>\angle\left(B1\right)=\angle\left(C1\right)=140^o\)(2 góc đồng vị)
\(=>\angle\left(C4\right)+\angle\left(C1\right)=180^o\left(ke-bu\right)=>\angle\left(C4\right)=180^o-140^0=40^o\)
Giải:
Ta có: a//b//ca//b//c
=>∠(A1)+∠(B2)=180o=>∠(A1)+∠(B2)=180o(2 góc ở vị trí trong cùng phía)
=>∠(B2)=1800−1400=40o=>∠(B2)=1800−1400=40o
có ∠(B3)+∠(B2)=180o(ke−bu)∠(B3)+∠(B2)=180o(ke−bu)
=>∠(B3)=1800−400=140o=>∠(B3)=1800−400=140o
b, ∠(B2)+∠(B1)=180o(ke−bu)∠(B2)+∠(B1)=180o(ke−bu)
=>∠(B1)=180o−40o=140o=>∠(B1)=180o−40o=140o
b//c=>∠(B1)=∠(C1)=140ob//c=>∠(B1)=∠(C1)=140o(2 góc đồng vị)
=>∠(C4)+∠(C1)=180o(ke−bu)=>∠(C4)=180o−1400=40o