HP
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
7 tháng 11 2021
a, Vì a//b và a⊥AB nên b⊥AB
b, Vì a//b nên \(\widehat{CDB}=180^0-\widehat{ACD}=60^0\) (trong cùng phía)
Vì a//b nên \(\widehat{CDB}=\widehat{aCD}=60^0\) (so le trong)
7 tháng 11 2021
dễ mà
a.a//b,a vuông góc với AB
=>b vuông góc với AB
b.Tính CDB bằng cách dựa vào tc góc trong cùng phía
tính aCD bằng cách dựa vào tc kề bù
1D
0
22 tháng 7 2021
Bài 3:
a) Ta có: \(A-\left(9x^3+8x^2-2x-7\right)=-9x^3-8x^2+5x+11\)
\(\Leftrightarrow A=-9x^3-8x^2+5x+11+9x^3+8x^2-2x-7\)
\(\Leftrightarrow A=3x+4\)
b) Đặt A(x)=0
nên 3x+4=0
hay \(x=-\dfrac{4}{3}\)
22 tháng 7 2021
Bạn có biết giải bài hình k giúp mình với 21:00 mình phải nộp rồi
8 tháng 11 2021
Gọi số vở 7A,7B,7C ll là a,b,c(quyển;a,b,c∈N*)
Áp dụng tc dstbn:
\(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{4}=\dfrac{a+c}{2+4}=\dfrac{120}{8}=15\\ \Rightarrow\left\{{}\begin{matrix}a=30\\b=45\\c=60\end{matrix}\right.\)
Vậy ...
YN
2
H
28 tháng 4 2022
1)
a. Xét tg ABC cân tại A có AC=AB; gACB = g ABC.
Xét tg ACN và tg ABM có:
CN=BM (gt)
AC=AB
gACB=gABC
=> tg ACN = tg ABM (cgc)
=> AN=AM (2 cạnh tg ứng)
H là trung điểm BC nên AH là đường trung tuyến của tg ABC
Mak tg ABC cân => H cũng là đường cao của tg ABC => AH ⊥ BC
b. Vì H là trung đ của BC nên CH=HB=BC/2= 3cm
Áp dụng định lý Py ta go vào tg AHB có:
AB^2=AH^2+HB^2
AH^2= AB^2 - HB^2
AH^2= 5^2 - 3^2 = 16 cm
=> AH= 4 cm
c. Xét tg AMN và tg KMB có:
AM=KM (gt)
MN=BM (gt)
gHMA=gKMB (đối đỉnh)
=> tg AMN = tg KMB (cgc)
d. tg AMN = tg KMB => gMAN=gMKB
=> AN=KB=Am
Mà AB>AM (quan hệ giữ đường xiêng và hình chiếu) nên AB>BK
=> gBKA> gBAK
=> gMAN>gBAM
TM
8 tháng 11 2021
a/ Ta có: \(\begin{matrix}a\text{ // }b\\a\perp AB\end{matrix}\Rightarrow b\perp AB\)
b/ \(\hat{ACD}+\hat{CDB}=180^o\) (trong cùng phía, a // b)
\(\Rightarrow\hat{CDB}=180^o-\hat{ACD}=60^o\)
\(\hat{ACD}+\hat{aCD}=180^o\) (kề bù)
\(\Rightarrow\hat{aCD}=180^o-\hat{ACD}=60^o\)
HP
16 tháng 9 2021
4. \(\dfrac{-3}{2}+x-\dfrac{5}{4}=\dfrac{-1}{3}-2x\)
<=> \(\dfrac{-18}{12}+\dfrac{12x}{12}-\dfrac{15}{12}=\dfrac{-4}{12}-\dfrac{24x}{12}\)
<=> -18 + 12x - 15 = -4 - 24x
<=> 12x + 24x = 18 + 15 - 4
<=> 36x = 29
<=> x = \(\dfrac{29}{36}\)
6. \(\dfrac{3}{4}x-\dfrac{3}{2}=\dfrac{5}{6}+\dfrac{3}{8}x\)
<=> \(\dfrac{18x}{24}-\dfrac{36}{24}=\dfrac{20}{24}+\dfrac{9x}{24}\)
<=> 18x - 36 = 20 + 9x
<=> 18x - 9x = 20 + 36
<=> 9x = 56
<=> x = \(\dfrac{56}{9}\)
7. \(3-\left(\dfrac{1}{2}+2x\right)=\dfrac{2}{3}-x\)
<=> \(3-\dfrac{1}{2}-2x=\dfrac{2}{3}-x\)
<=> \(\dfrac{18}{6}-\dfrac{3}{6}-\dfrac{12x}{6}=\dfrac{4}{6}-\dfrac{6x}{6}\)
<=> 18 - 3 - 12x = 4 - 6x
<=> 15 - 4 = 12x - 6x
<=> 11 = 6x
<=> x = \(\dfrac{11}{6}\)
BT
20 tháng 7 2023
Để chứng minh rằng 2 tia phân giác 2 góc đối đỉnh là 2 tia đối nhau, chúng ta cần sử dụng một số khái niệm và định lý trong hình học. Dưới đây là cách chứng minh:
Giả sử chúng ta có hai tia AB và AC, và chúng phân giác hai góc đối đỉnh, tức là góc BAC và góc CAD. Chúng ta cần chứng minh rằng hai tia AB và AC là hai tia đối nhau.
Để chứng minh điều này, ta sẽ sử dụng Định lý Tia Phân Giác (Bisector Theorem) và Định lý Tia Tiếp Tuyến (Alternate Segment Theorem) như sau:
Bước 1: Vẽ đường thẳng đi qua điểm A và song song với tia BC (đường thẳng đó gọi là đường thẳng d).
Bước 2: Do AB là tia phân giác góc BAC, nên theo Định lý Tia Phân Giác, ta có: AB/BD = AC/CD
Bước 3: Do AC là tia phân giác góc CAD, nên theo Định lý Tia Phân Giác, ta có: AC/CD = AB/BD
Bước 4: Từ Bước 2 và Bước 3, ta có: AB/BD = AC/CD = AB/BD Bước 5: Từ Bước 4, ta suy ra AB = AC.
Vậy, chúng ta đã chứng minh rằng hai tia AB và AC là hai tia đối nhau. Hy vọng cách chứng minh trên giúp bạn hiểu và giải đúng bài tập.
BT
19 tháng 7 2023
Để chứng minh rằng 2 tia phân giác 2 góc đối đỉnh là 2 tia đối nhau, chúng ta cần sử dụng một số khái niệm và định lý trong hình học. Dưới đây là cách chứng minh:
Giả sử chúng ta có hai tia AB và AC, và chúng phân giác hai góc đối đỉnh, tức là góc BAC và góc CAD. Chúng ta cần chứng minh rằng hai tia AB và AC là hai tia đối nhau.
Để chứng minh điều này, ta sẽ sử dụng Định lý Tia Phân Giác (Bisector Theorem) và Định lý Tia Tiếp Tuyến (Alternate Segment Theorem) như sau:
Bước 1: Vẽ đường thẳng đi qua điểm A và song song với tia BC (đường thẳng đó gọi là đường thẳng d).
Bước 2: Do AB là tia phân giác góc BAC, nên theo Định lý Tia Phân Giác, ta có: AB/BD = AC/CD
Bước 3: Do AC là tia phân giác góc CAD, nên theo Định lý Tia Phân Giác, ta có: AC/CD = AB/BD
Bước 4: Từ Bước 2 và Bước 3, ta có: AB/BD = AC/CD = AB/BD Bước 5: Từ Bước 4, ta suy ra AB = AC.
Vậy, chúng ta đã chứng minh rằng hai tia AB và AC là hai tia đối nhau. Hy vọng cách chứng minh trên giúp bạn hiểu và giải đúng bài tập.
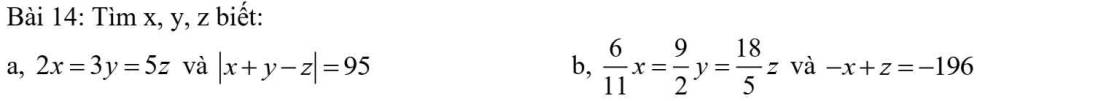
a:
2x=3y=5z
=>\(\dfrac{2x}{30}=\dfrac{3y}{30}=\dfrac{5z}{30}\)
=>\(\dfrac{x}{15}=\dfrac{y}{10}=\dfrac{z}{6}\)
Đặt \(\dfrac{x}{15}=\dfrac{y}{10}=\dfrac{z}{6}=k\)
=>x=15k; y=10k; z=6k
|x+y-z|=95
=>|15k+10k-6k|=95
=>|19k|=95
=>|k|=5
=>\(\left[{}\begin{matrix}k=5\\k=-5\end{matrix}\right.\)
TH1: k=5
=>\(x=15\cdot5=75;y=10\cdot5=50;z=6\cdot5=30\)
TH2: k=-5
=>\(x=15\cdot\left(-5\right)=-75;y=10\cdot\left(-5\right)=-50;z=6\cdot\left(-5\right)=-30\)
b: \(\dfrac{6}{11}x=\dfrac{9}{2}y=\dfrac{18}{5}z\)
=>\(\dfrac{x}{\dfrac{11}{6}}=\dfrac{y}{\dfrac{2}{9}}=\dfrac{z}{\dfrac{5}{18}}\)
mà -x+z=-196
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{\dfrac{11}{6}}=\dfrac{y}{\dfrac{2}{9}}=\dfrac{z}{\dfrac{5}{18}}=\dfrac{-x+z}{-\dfrac{11}{6}+\dfrac{5}{18}}=\dfrac{-196}{-\dfrac{14}{9}}=126\)
=>\(x=126\cdot\dfrac{11}{6}=231;y=126\cdot\dfrac{2}{9}=28;z=126\cdot\dfrac{5}{18}=35\)