
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



5:
a: góc ACB=1/2*180=90 độ
Xét ΔAKH vuông tại K và ΔACB vuông tại A có
góc KAH chung
=>ΔAKH đồng dạng với ΔACB
b: Xét ΔADC và ΔBEC có
AD=BE
góc DAC=góc EBC
AC=BC
=>ΔADC=ΔBEC
=>DC=EC
=>ΔDEC cân tại C
góc CAB=45 độ
=>góc CDE=góc CAB=45 độ
=>ΔCDE vuông cân tại C

CÁi này easy mà .-.
\(\frac{\sqrt[3]{7-x}-\sqrt[3]{x-5}}{\sqrt[3]{7-x}+\sqrt[3]{x-5}}=6-x\)
\(\Leftrightarrow\frac{\frac{\left(7-x\right)-\left(x-5\right)}{\left(\sqrt[3]{7-x}\right)^2+\left(\sqrt[3]{x-5}\right)^2+\sqrt[3]{7-x}\sqrt[3]{x-5}}}{\sqrt[3]{7-x}+\sqrt[3]{x-5}}+\left(x-6\right)=0\)
\(\Leftrightarrow\frac{\frac{-2\left(x-6\right)}{\left(\sqrt[3]{7-x}\right)^2+\left(\sqrt[3]{x-5}\right)^2+\sqrt[3]{7-x}\sqrt[3]{x-5}}}{\sqrt[3]{7-x}+\sqrt[3]{x-5}}+\left(x-6\right)=0\)
\(\Leftrightarrow\left(x-6\right)\left(\frac{\frac{-2}{\left(\sqrt[3]{7-x}\right)^2+\left(\sqrt[3]{x-5}\right)^2+\sqrt[3]{7-x}\sqrt[3]{x-5}}}{\sqrt[3]{7-x}+\sqrt[3]{x-5}}+1\right)=0\)
\(\Rightarrow x-6=0\Rightarrow x=6\)

Bài 4:
a: Xét tứ giác OBAC có
\(\widehat{OBA}+\widehat{OCA}=180^0\)
Do đó: OBAC là tứ giác nội tiếp
b: Xét (O) có
AB là tiếp tuyến
AC là tiếp tuyến
Do đó: AB=AC
hay A nằm trên đường trung trực của BC(1)
Ta có: OB=OC
nên O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra OA là đường trung trực của BC
hay OA⊥BC
c: Xét ΔOBA vuông tại B có BA là đường cao
nên \(OH\cdot OA=OB^2=R^2\)

1:
AC=căn 5^2-3^2=4cm
BH=AB^2/BC=1,8cm
CH=5-1,8=3,2cm
AH=3*4/5=2,4cm
2:
ΔCBA vuông tại B có tan 40=BC/BA
=>BC/10=tan40
=>BC=8,39(m)
ΔCBD vuông tại B có tan D=BC/BD
=>BD=8,39/tan35=11,98(m)

Câu 2:
Ta có: \(x^2-2\left(m+1\right)x+m^2+4=0\)
a=1; b=-2m-2; \(c=m^2+4\)
\(\text{Δ}=b^2-4ac\)
\(=\left(-2m-2\right)^2-4\cdot\left(m^2+4\right)\)
\(=4m^2+8m+4-4m^2-16\)
=8m-12
Để phương trình có hai nghiệm phân biệt thì Δ>0
\(\Leftrightarrow8m>12\)
hay \(m>\dfrac{3}{2}\)
Áp dụng hệ thức Vi-et, ta được:
\(\left\{{}\begin{matrix}x_1+x_2=2\left(m+1\right)=2m+2\\x_1x_2=m^2+4\end{matrix}\right.\)
Vì x1 là nghiệm của phương trình nên ta có:
\(x_1^2-2\left(m+1\right)\cdot x_1+m^2+4=0\)
\(\Leftrightarrow x_1^2=2\left(m+1\right)x_1-m^2-4\)
Ta có: \(x_1^2+2\left(m+1\right)x_2=2m^2+20\)
\(\Leftrightarrow2\left(m+1\right)x_1-m^2-4+2\left(m+1\right)x_2-2m^2-20=0\)
\(\Leftrightarrow2\left(m+1\right)\left(x_1+x_2\right)-3m^2-24=0\)
\(\Leftrightarrow2\left(m+1\right)\cdot\left(2m+2\right)-3m^2-24=0\)
\(\Leftrightarrow4m^2+8m+4-3m^2-24=0\)
\(\Leftrightarrow m^2+8m-20=0\)
Đến đây bạn tự tìm m là xong rồi

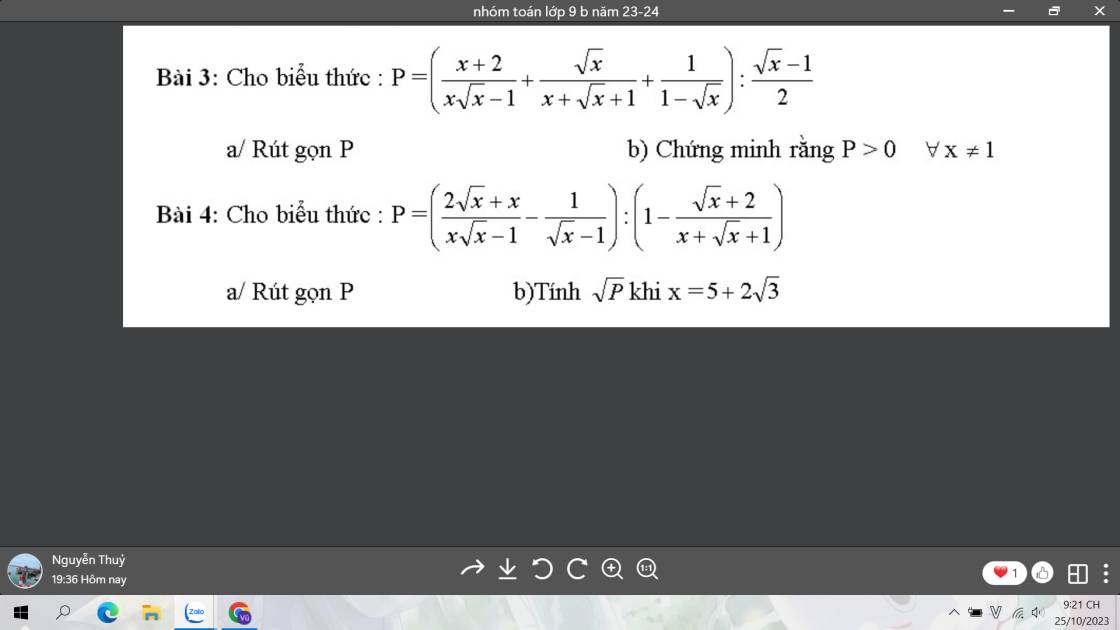 giải giúp mik bài 3 nha mn <3
giải giúp mik bài 3 nha mn <3









3:
ĐKXĐ: x>=0; x<>1
a: \(P=\left(\dfrac{x+2}{x\sqrt{x}-1}+\dfrac{\sqrt{x}}{x+\sqrt{x}+1}+\dfrac{1}{1-\sqrt{x}}\right):\dfrac{\sqrt{x}-1}{2}\)
\(=\left(\dfrac{x+2}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}+\dfrac{\sqrt{x}}{x+\sqrt{x}+1}-\dfrac{1}{\sqrt{x}-1}\right)\cdot\dfrac{2}{\sqrt{x}-1}\)
\(=\dfrac{x+2+x-\sqrt{x}-x-\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\cdot\dfrac{2}{\sqrt{x}-1}\)
\(=\dfrac{x-2\sqrt{x}+1}{\left(\sqrt{x}-1\right)^2}\cdot\dfrac{2}{x+\sqrt{x}+1}=\dfrac{2}{x+\sqrt{x}+1}\)
b: \(x+\sqrt{x}+1=\sqrt{x}\left(\sqrt{x}+1\right)+1>=0+1=1\)
=>\(x+\sqrt{x}+1>0\forall x\) thỏa mãn ĐKXĐ
mà 2>0
nên \(P=\dfrac{2}{x+\sqrt{x}+1}>0\forall x\) thỏa mãn ĐKXĐ
thank