K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 3 2022
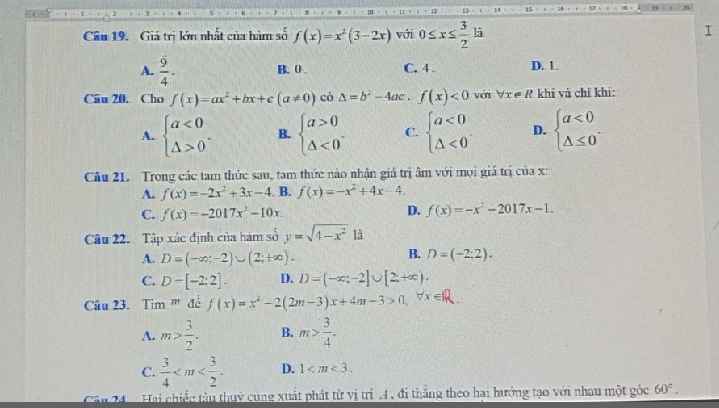
19.
\(f\left(x\right)=x^2\left(3-2x\right)=x.x.\left(3-2x\right)\le\left(\dfrac{x+x+3-2x}{3}\right)^3=1\)
\(\Rightarrow\max\limits_{\left[0;\dfrac{3}{2}\right]}f\left(x\right)=1\)
20.
\(f\left(x\right)< 0;\forall x\in R\Leftrightarrow\left\{{}\begin{matrix}a< 0\\\Delta< 0\end{matrix}\right.\)
21.
A là đáp án đúng, do đa thức \(f\left(x\right)=-2x^2+3x-4\) có:
\(\left\{{}\begin{matrix}a=-2< 0\\\Delta=3^2-4.\left(-2\right).\left(-4\right)=-23< 0\end{matrix}\right.\)
22.
ĐKXĐ: \(4-x^2\le0\Rightarrow\left(2-x\right)\left(2+x\right)\le0\)
\(\Rightarrow-2\le x\le2\Rightarrow D=\left[-2;2\right]\)
23.
\(f\left(x\right)>0;\forall x\Leftrightarrow\left\{{}\begin{matrix}a=1>0\\\Delta'=\left(2m-3\right)^2-\left(4m-3\right)< 0\end{matrix}\right.\)
\(\Leftrightarrow4m^2-16m+12< 0\)
\(\Rightarrow1< m< 3\)
CG
giúp mình với giải thích cho mình luôn nhé huhu mình cảm ơn
2
H
14 tháng 7 2023
10.D
Giải thích: Số chính phương là những số có chữ số tận cùng là 0,1,4,5,6,9.
Giả sử (2) là mệnh đề đúng: chữ số tận cùng của n là 4
Xét vào (1) thì là mệnh đề sai vì số tận cùng của n là 4 + 8 = 2 (Không phải số cp)
Xét vào (3) thì là mệnh đề sai vì số tận cùng của n là 4 - 1 = 3 (Không phải số cp)
Nhưng theo đề thì có 1 mệnh đề sai và 2 mệnh đề đúng.
Vậy giả sử nêu trên là sai. => Chọn D
NN
1
HP
19 tháng 3 2021
ĐK: \(x\ge0\)
Dễ thấy \(1-\sqrt{2\left(x^2-x+1\right)}\le1-\sqrt{2}< 0\)
Khi đó bất phương trình tương đương:
\(x-\sqrt{x}\le1-\sqrt{2\left(x^2-x+1\right)}\)
\(\Leftrightarrow\sqrt{x}-\dfrac{1}{\sqrt{x}}-1+\sqrt{2\left(x+\dfrac{1}{x}-1\right)}\le0\)
\(\Leftrightarrow\sqrt{x}-\dfrac{1}{\sqrt{x}}-1+\sqrt{2\left(\sqrt{x}-\dfrac{1}{\sqrt{x}}\right)^2+2}\le0\)
\(\Leftrightarrow t-1+\sqrt{2t^2+2}\le0\)
NV
Nguyễn Việt Lâm
Giáo viên
29 tháng 12 2021
\(\Delta'=4-m\)
a. Phương trình vô nghiệm khi:
\(4-m< 0\Rightarrow m>4\)
b. Phương trình có 2 nghiệm pb khi: \(4-m>0\Rightarrow m< 4\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=4\\x_1x_2=m\end{matrix}\right.\)
Không mất tính tổng quát, giả sử \(x_1=2x_2\)
\(\Rightarrow2x_2+x_2=4\Rightarrow x_2=\dfrac{4}{3}\Rightarrow x_1=\dfrac{8}{3}\)
\(\Rightarrow m=x_1x_2=\dfrac{32}{9}\)