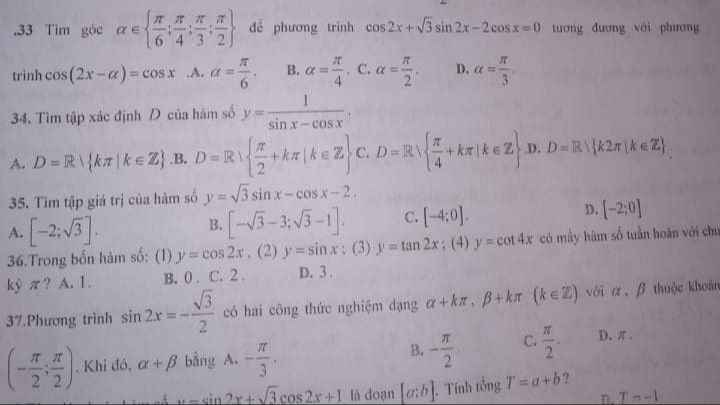K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NT
1
NT
5
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 10 2021
b.
\(\Leftrightarrow\dfrac{1}{2}cosx-\dfrac{\sqrt{3}}{2}sinx=-\dfrac{1}{2}\)
\(\Leftrightarrow cos\left(x+\dfrac{\pi}{3}\right)=-\dfrac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{\pi}{3}=\dfrac{2\pi}{3}+k2\pi\\x+\dfrac{\pi}{3}=-\dfrac{2\pi}{3}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{3}+k2\pi\\x=-\pi+k2\pi\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 10 2021
c.
\(\Leftrightarrow\dfrac{3}{5}sinx-\dfrac{4}{5}cosx=1\)
Đặt \(\dfrac{3}{5}=cosa\) với \(a\in\left(0;\dfrac{\pi}{2}\right)\Rightarrow\dfrac{4}{5}=sina\)
Pt trở thành:
\(sinx.cosa-cosx.sina=1\)
\(\Leftrightarrow sin\left(x-a\right)=1\)
\(\Leftrightarrow x-a=\dfrac{\pi}{2}+k2\pi\)
\(\Leftrightarrow x=a+\dfrac{\pi}{2}+k2\pi\)
NV
Nguyễn Việt Lâm
Giáo viên
16 tháng 7 2021
33.
\(\dfrac{1}{2}cos2x+\dfrac{\sqrt{3}}{2}sin2x=cosx\)
\(\Leftrightarrow cos\left(2x-\dfrac{\pi}{3}\right)=cosx\)
So sánh nó với \(cos\left(2x-a\right)=cosx\)
\(\Rightarrow a=\dfrac{\pi}{3}\)
34.
ĐKXĐ:
\(sinx-cosx\ne0\)
\(\Leftrightarrow tanx\ne1\)
\(\Leftrightarrow x\ne\dfrac{\pi}{4}+k\pi\)
NV
Nguyễn Việt Lâm
Giáo viên
16 tháng 7 2021
35.
\(y=2\left(\dfrac{\sqrt{3}}{2}sinx-\dfrac{1}{2}cosx\right)-2=2sin\left(x-\dfrac{\pi}{6}\right)-2\)
Do \(-1\le sin\left(x-\dfrac{\pi}{6}\right)\le1\Rightarrow-4\le y\le0\)
Tập giá trị: \(\left[-4;0\right]\)
36.
\(y=cos2x\) tuần hoàn chu kì \(\dfrac{2\pi}{\left|2\right|}=\pi\)
\(y=sinx\) tuàn hoàn chu kì \(\dfrac{2\pi}{\left|1\right|}=2\pi\)
\(y=tan2x\) tuần hoàn chu kì \(\dfrac{\pi}{\left|2\right|}=\dfrac{\pi}{2}\)
\(y=cot4x\) tuần hoàn chu kì \(\dfrac{\pi}{\left|4\right|}=\dfrac{\pi}{4}\)
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 9 2021
1. ĐKXĐ:
a. \(sin\left(x+\dfrac{\pi}{3}\right)\ne0\Rightarrow x+\dfrac{\pi}{3}\ne k\pi\Rightarrow x\ne-\dfrac{\pi}{3}+k\pi\)
b. \(cos\left(x-\dfrac{\pi}{4}\right)\ne0\Rightarrow x-\dfrac{\pi}{4}\ne\dfrac{\pi}{2}+k\pi\Rightarrow x\ne\dfrac{3\pi}{4}+k\pi\)
2.
a.
\(-1\le sinx\le1\Rightarrow-5\le-5sinx\le5\Rightarrow-3\le y\le8\)
Tập giá trị: \(\left[-3;8\right]\)
b.
\(-1\le cos2x\le1\Rightarrow-4\le4cos2x\le4\Rightarrow3\le y\le11\)
Tập giá trị: \(\left[3;11\right]\)
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 11 2021
\(2cos\left(x+\dfrac{\pi}{6}\right)-1=0\Rightarrow cos\left(x+\dfrac{\pi}{6}\right)=\dfrac{1}{2}\)
\(\Rightarrow\left[{}\begin{matrix}x+\dfrac{\pi}{6}=\dfrac{\pi}{3}+k2\pi\\x+\dfrac{\pi}{6}=-\dfrac{\pi}{3}+n2\pi\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+k2\pi\\x=-\dfrac{\pi}{2}+n2\pi\end{matrix}\right.\)
\(\left\{{}\begin{matrix}-\dfrac{\pi}{2}\le\dfrac{\pi}{6}+k2\pi< 2\pi\\-\dfrac{\pi}{2}\le-\dfrac{\pi}{2}+n2\pi< 2\pi\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}-\dfrac{1}{3}\le k< \dfrac{11}{12}\\0\le n< \dfrac{5}{4}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}k=\left\{0\right\}\\n=\left\{0;1\right\}\end{matrix}\right.\) \(\Rightarrow x=\left\{\dfrac{\pi}{6};-\dfrac{\pi}{2};\dfrac{3\pi}{2}\right\}\Rightarrow\dfrac{\pi}{6}-\dfrac{\pi}{2}+\dfrac{3\pi}{2}=\dfrac{7\pi}{6}\)
LN
2
HP
10 tháng 9 2021
3.
\(4sinx+cosx+2cos\left(x+\dfrac{\pi}{3}\right)=2\)
\(\Leftrightarrow4sinx+cosx+cosx-\sqrt{3}sinx=2\)
\(\Leftrightarrow\left(4-\sqrt{3}\right)sinx+2cosx=2\)
\(\Leftrightarrow\sqrt{23-4\sqrt{3}}\left(\dfrac{4-\sqrt{3}}{\sqrt{23-4\sqrt{3}}}sinx+\dfrac{2}{\sqrt{23-4\sqrt{3}}}cosx\right)=2\)
\(\Leftrightarrow cos\left(x-arccos\dfrac{2}{\sqrt{23-4\sqrt{3}}}\right)=\dfrac{2}{\sqrt{23-4\sqrt{3}}}\)
\(\Leftrightarrow x-arccos\dfrac{2}{\sqrt{23-4\sqrt{3}}}=\pm arccos\dfrac{2}{\sqrt{23-4\sqrt{3}}}+k2\pi\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2arccos\dfrac{2}{\sqrt{23-4\sqrt{3}}}+k2\pi\\x=k2\pi\end{matrix}\right.\)
HP
10 tháng 9 2021
4.
\(sinx+2cos\left(x+\dfrac{\pi}{3}\right)+4sin\left(x+\dfrac{\pi}{6}\right)+cosx=4\)
\(\Leftrightarrow sinx+cosx-\sqrt{3}sinx+2\sqrt{3}sinx+2cosx+cosx=4\)
\(\Leftrightarrow\left(1+\sqrt{3}\right)sinx+4cosx=4\)
\(\Leftrightarrow\sqrt{20+2\sqrt{3}}\left(\dfrac{1+\sqrt{3}}{\sqrt{20+2\sqrt{3}}}sinx+\dfrac{4}{\sqrt{20+2\sqrt{3}}}cosx\right)=4\)
\(\Leftrightarrow cos\left(x-arccos\dfrac{4}{\sqrt{20+2\sqrt{3}}}\right)=\dfrac{4}{\sqrt{20+2\sqrt{3}}}\)
\(\Leftrightarrow x-arccos\dfrac{4}{\sqrt{20+2\sqrt{3}}}=\pm arccos\dfrac{4}{\sqrt{20+2\sqrt{3}}}+k2\pi\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2arccos\dfrac{4}{\sqrt{20+2\sqrt{3}}}+k2\pi\\x=k2\pi\end{matrix}\right.\)
DN
1