K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
AH
Akai Haruma
Giáo viên
12 tháng 7 2021
Lời giải:
Đẳng thức \(\Leftrightarrow \frac{n!}{(n-2)!}-\frac{(n+1)!}{(n-1)!2!}=5\)
\(\Leftrightarrow n(n-1)-\frac{n(n+1)}{2}=5\)
\(\Leftrightarrow n^2-3n-10=0\Leftrightarrow (n-5)(n+2)=0\)
Vì $n$ tự nhiên nên $n=5$. Đáp án B.
AH
Akai Haruma
Giáo viên
11 tháng 7 2021
Bạn lưu ý chuyển bài toán vào đúng mục xác suất trong toán 11, không phải hàm số lượng giác.
AH
Akai Haruma
Giáo viên
11 tháng 7 2021
Lời giải:
Gọi số có 3 chữ số phân biệt được lập từ $0,1,2,3$ là $\overline{a_1a_2a_3}$.
$A$ là tập hợp các số $\overline{a_1a_2a_3}$ mà $a_1$ có thể bằng $0,1,2,3$
$B$ là tập hợp các số $\overline{a_1a_2a_3}$ mà $a_1\neq 0$ (chính là số thỏa đề)
$C$ là tập các số $\overline{a_1a_2a_3}$ mà $a_1=0$
Tại tập $A$ thì mỗi số $0,1,2,3$ xuất hiện $18$ lần ở 3 vị trí hàng chục, trăm, đơn vị.
Tổng chữ số tập $A$:
$\frac{1}{3}.18(0+1+2+3)(10^2+10+1)=3996$
Tổng chữ số tập $C$ là:
$012+021+013+031+023+032=132$
Tồng các chữ số tập $B$ là:
$3996-132=3864$
Tổng các chữ số tập $B$:
$11988-132=11856$
29 tháng 6 2021
Đk:\(tanx\ne\pm1;tanx\ne0;sin\left(x+\dfrac{\pi}{4}\right)\ne0\)
Pt \(\Leftrightarrow\dfrac{\dfrac{sinx}{cosx}}{1-\dfrac{sin^2x}{cos^2x}}=\dfrac{1}{2}.cotx\left(x+\dfrac{\pi}{4}\right)\)
\(\Leftrightarrow\dfrac{sinx.cosx}{cos^2x-sin^2x}=\dfrac{1}{2}.cotx\left(x+\dfrac{\pi}{4}\right)\)
\(\Leftrightarrow\dfrac{\dfrac{1}{2}.sin2x}{cos2x}=\dfrac{1}{2}.tan\left(\dfrac{\pi}{4}-x\right)\)
\(\Leftrightarrow tan2x=tan\left(\dfrac{\pi}{4}-x\right)\)
\(\Leftrightarrow2x=\dfrac{\pi}{4}-x+k\pi\), k nguyên
\(\Leftrightarrow x=\dfrac{\pi}{12}+k.\dfrac{\pi}{3}\)
Ý D
NV
Nguyễn Việt Lâm
Giáo viên
30 tháng 6 2021
Đặt \(x-\dfrac{\pi}{4}=t\Rightarrow x=t+\dfrac{\pi}{4}\Rightarrow3x-\dfrac{\pi}{4}=3\left(t+\dfrac{\pi}{4}\right)-\dfrac{\pi}{4}=3t+\dfrac{\pi}{2}\)
\(\Rightarrow sin\left(3x-\dfrac{\pi}{4}\right)=sin\left(3t+\dfrac{\pi}{4}\right)=cos3t\)
Đồng thời: \(sin^4x+cos^4x=\left(sin^2x+cos^2x\right)^2-2sin^2x.cos^2x\)
\(=1-\dfrac{1}{2}sin^22x=1-\dfrac{1}{2}sin^2\left(2t+\dfrac{\pi}{2}\right)=1-\dfrac{1}{2}cos^22t\)
Nên pt trở thành:
\(1-\dfrac{1}{2}cos^22t+cost.cos3t-\dfrac{3}{2}=0\)
\(\Leftrightarrow-1-cos^22t+cos4t+cos2t=0\)
\(\Leftrightarrow-1-cos^22t+2cos^22t-1+cos2t=0\)
\(\Leftrightarrow cos^22t+cos2t-2=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos2t=1\\cos2t=-2\left(loại\right)\end{matrix}\right.\)
\(\Leftrightarrow2t=k2\pi\)
\(\Leftrightarrow t=k\pi\)
\(\Leftrightarrow x-\dfrac{\pi}{4}=k\pi\)
\(\Leftrightarrow x=\dfrac{\pi}{4}+k\pi\)
HD
1
KB
1 tháng 5 2022
Ta có : \(f\left(2\right)=2a+b-6\)
\(\lim\limits_{x\rightarrow2^+}\dfrac{x-\sqrt{x+2}}{x^2-4}=\lim\limits_{x\rightarrow2^+}\dfrac{x^2-x-2}{\left(x-2\right)\left(x+2\right)\left(x+\sqrt{x+2}\right)}\)
\(=\lim\limits_{x\rightarrow2^+}\dfrac{x+1}{\left(x+2\right)\left(x+\sqrt{x+2}\right)}=\dfrac{3}{16}\)
\(\lim\limits_{x\rightarrow2^-}x^2+ax+3b=4+2a+3b\)
H/s liên tục tại điểm x = 2 \(\Leftrightarrow\dfrac{3}{16}=2a+3b+4=2a+b-6\)
Suy ra : \(a=\dfrac{179}{32};b=-5\) => t = a + b = 19/32 . Chọn C
HP
22 tháng 6 2021
\(sin\left(3x-\dfrac{\pi}{4}\right)=\dfrac{\sqrt{3}}{2}\)
\(\Leftrightarrow sin\left(3x-\dfrac{\pi}{4}\right)=sin\dfrac{\pi}{3}\)
\(\Leftrightarrow\left[{}\begin{matrix}3x-\dfrac{\pi}{4}=\dfrac{\pi}{3}+k2\pi\\3x-\dfrac{\pi}{4}=\pi-\dfrac{\pi}{3}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{7\pi}{36}+\dfrac{k2\pi}{3}\\x=\dfrac{11\pi}{36}+\dfrac{k2\pi}{3}\end{matrix}\right.\)
\(\Rightarrow\) Nghiệm âm lớn nhất: \(x_1=\dfrac{11\pi}{36}-\dfrac{2\pi}{3}=-\dfrac{13\pi}{36}\)
Nghiệm dương bé nhất: \(x_2=\dfrac{7\pi}{36}\)
\(\Rightarrow x_1+x_2=-\dfrac{\pi}{6}\)
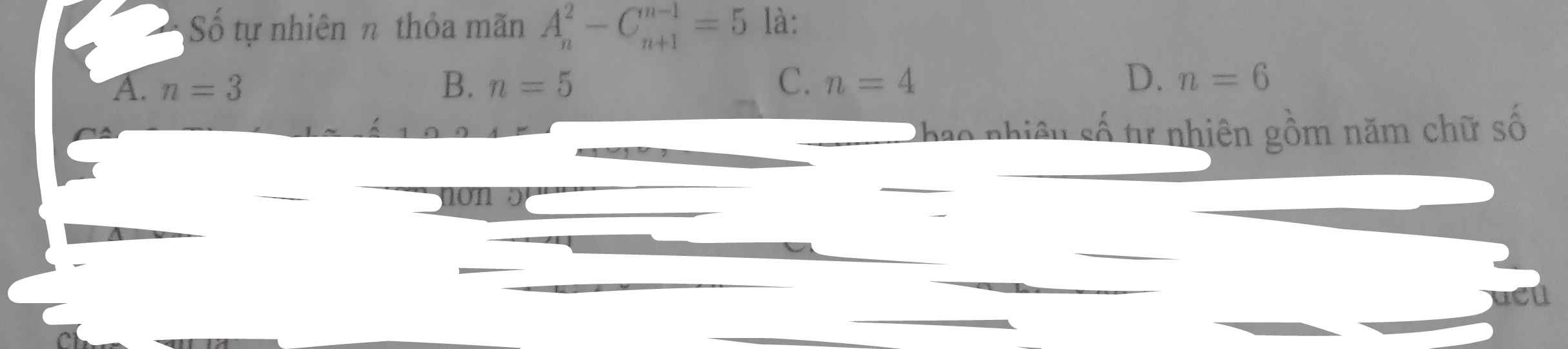
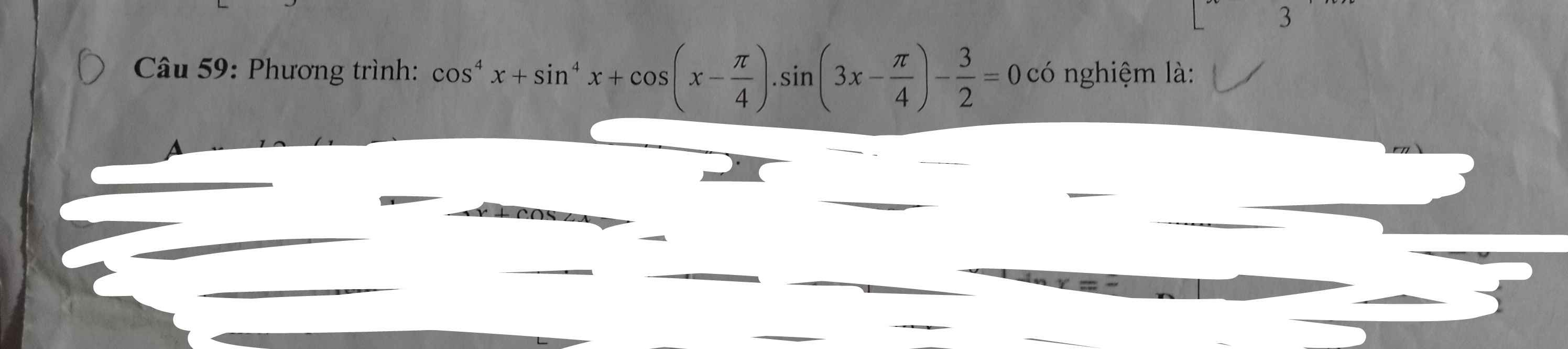
Có \(2!=2\) cách xếp 2 người nhóm 1 kề nhau
Có \(3!=6\) cách xếp 3 người nhóm 2 kề nhau
Coi 2 người nhóm 1 là 1 bó và 3 người nhóm 2 là 1 bó (chiếm 5 vị trí nên còn 2 vị trí trống trong 7 vị trí)
Chọn 2 vị trí trong 4 vị trí: \(A_4^2=12\) cách
Theo quy tắc nhân có: \(2.6.12=144\) cách