Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: x + 1 3 –x +1 = (x -1)(x -2)
⇔ x 3 +3 x 2 +3x +1 –x +1 = x 2 -2x –x +2
⇔ x 3 +2 x 2 +5x = 0 ⇔ x( x 2 + 2x + 5) =0
⇔ x =0 hoặc x 2 +2x +5 =0
Giải phương trình x 2 +2x +5 =0
∆ ’ = 1 2 - 1.5 = 1 - 5 = -4 < 0 ⇒ phương trình vô nghiệm
Vậy phương trình đã cho có 1 nghiệm : x=0

Ta có: x 3 – 5 x 2 –x +5 = 0 ⇔ x 2 ( x -5) – ( x -5) =0
⇔ (x -5)(x2 -1) =0 ⇔ (x -5)(x -1)(x +1) =0
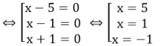
Vậy phương trình đã cho có 3 nghiệm :x1 = 5;x2 =1;x3=-1

Ta có: 3 x 3 +6 x 2 -4x =0 ⇔ x(3 x 2 +6x -4) =0
⇔ x = 0 hoặc 3 x 2 +6x -4 =0
Giải phương trình 3 x 2 +6x -4 =0
∆ ’ = 3 2 - 3(-4) = 9 + 12 = 21 > 0
∆ ' = 21
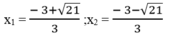
Vậy phương trình đã cho có 3 nghiệm
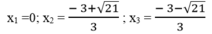

Ta có: x 2 + x + 1 2 = 4 x - 1 2
⇔ [( x 2 +x +1) + (4x -1 )] [( x 2 +x +1) - (4x -1 )]=0
⇔ ( x 2 +5x)( x 2 -3x +2) =0 ⇔ x(x+5) ( x 2 -3x +2) =0
⇔ x =0 hoặc x+5 =0 hoặc x2 -3x +2 =0
x+5 =0 ⇔ x=-5
x 2 -3x +2 =0
∆ = - 3 2 -4.2.1 = 9 -8 =1 > 0
∆ = 1 =1
![]()
Vậy phương trình đã cho có 4 nghiệm:
x 1 =0 ; x 2 =-5 ; x 3 =2 ; x 4 =1

(x2 + 2x – 5)2 = (x2 – x + 5)2
⇔ (x2 + 2x – 5)2 – (x2 – x + 5)2 = 0
⇔ [(x2 + 2x – 5) – (x2 – x + 5)].[(x2 + 2x – 5) + (x2 – x + 5)] = 0
⇔ (3x – 10)(2x2 + x ) = 0
⇔ (3x-10).x.(2x+1)=0
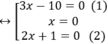
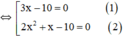
+ Giải (1): 3x – 10 = 0 ⇔ 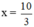
+ Giải (2):
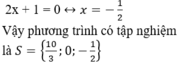

⇔ [( x 2 +x +1) + (4x -1 )] [( x 2 +x +1) - (4x -1 )]=0
∆ = - 3 2 -4.2.1 = 9 -8 =1 > 0
∆ = 1 =1
x 2 + 3 x + 2 2 = 6.( x 2 +3x +2)
⇔ x 2 + 3 x + 2 2 - 6.( x 2 +3x +2)=0
⇔ ( x 2 +3x + 2)[ ( x 2 +3x + 2) -6] =0
⇔ ( x 2 +3x + 2) .( x 2 +3x -4 )=0
x 2 +3x + 2 =0
Phương trình có dạng a –b +c =0 nên x 1 = -1 , x 2 =-2
x 2 +3x -4 =0
Phương trình có dạng a +b +c =0 nên x 1 = 1 , x 2 = -4
Vậy phương trình đã cho có 4 nghiệm :
x 1 = -1 , x 2 =-2 ; x 3 = 1 , x 4 =-4

a) (3x2 - 7x – 10)[2x2 + (1 - √5)x + √5 – 3] = 0
=> hoặc (3x2 - 7x – 10) = 0 (1)
hoặc 2x2 + (1 - √5)x + √5 – 3 = 0 (2)
Giải (1): phương trình a - b + c = 3 + 7 - 10 = 0
nên
x1 = - 1, x2 = =
Giải (2): phương trình có a + b + c = 2 + (1 - √5) + √5 - 3 = 0
nên
x3 = 1, x4 =
b) x3 + 3x2– 2x – 6 = 0 ⇔ x2(x + 3) – 2(x + 3) = 0 ⇔ (x + 3)(x2 - 2) = 0
=> hoặc x + 3 = 0
hoặc x2 - 2 = 0
Giải ra x1 = -3, x2 = -√2, x3 = √2
c) (x2 - 1)(0,6x + 1) = 0,6x2 + x ⇔ (0,6x + 1)(x2 – x – 1) = 0
=> hoặc 0,6x + 1 = 0 (1)
hoặc x2 – x – 1 = 0 (2)
(1) ⇔ 0,6x + 1 = 0
⇔ x2 = =
(2): ∆ = (-1)2 – 4 . 1 . (-1) = 1 + 4 = 5, √∆ = √5
x3 = , x4 =
Vậy phương trình có ba nghiệm:
x1 = , x2 =
, x3 =
,
d) (x2 + 2x – 5)2 = ( x2 – x + 5)2 ⇔ (x2 + 2x – 5)2 - ( x2 – x + 5)2 = 0
⇔ (x2 + 2x – 5 + x2 – x + 5)( x2 + 2x – 5 - x2 + x - 5) = 0
⇔ (2x2 + x)(3x – 10) = 0
⇔ x(2x + 1)(3x – 10) = 0
Hoặc x = 0, x = , x =
Vậy phương trình có 3 nghiệm:
x1 = 0, x2 = , x3 =

x3 + 3x2 + 2x = 0 ⇔ x(x2 + 3x + 2) = 0
⇔ x = 0 hoặc x2 + 3x + 2 = 0 (1)
Giải phương trình (1) ta được các nghiệm x = -1; x = -2
Vậy phương trình đã cho có 3 nghiệm x = 0; x = -1; x = -2

x 3 + 3 x 2 + 2 x = 0 ⇔ x ( x 2 + 3 x + 2 ) = 0
⇔ x = 0 hoặc x 2 + 3 x + 2 = 0 ( 1 )
Giải phương trình (1) ta được các nghiệm x = -1; x = -2
Vậy phương trình đã cho có 3 nghiệm x = 0; x = -1; x = -2
Ta có: 2 x 2 + 3 2 -10 x 3 -15x =0 ⇔ 2 x 2 + 3 2 - 5x(2 x 2 +3)=0
⇔ (2 x 2 +3)( 2 x 2 +3 - 5x) = 0 ⇔ (2 x 2 +3)( 2 x 2 - 5x +3)=0
Vì 2 x 2 ≥ 0 nên 2 x 2 +3 > 0
Suy ra : 2x2 - 5x +3=0
∆ = - 5 2 -4.2.3 =25 -24=1 > 0
∆ = 1 = 1
vậy phương trình đã cho có 2 nghiệm: x1 = 3/2 ; x2 = 1