Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(a,f'\left(x\right)=3x^2-6x\\ f'\left(x\right)\le0\Leftrightarrow3x^2-6x\le0\\ \Leftrightarrow3x\left(x-2\right)\le0\Leftrightarrow0\le x\le2\)
Lời giải:
a. $f'(x)\leq 0$
$\Leftrightarrow 3x^2-6x\leq 0$
$\Leftrightarrow x(x-2)\leq 0$
$\Leftrightarrow 0\leq x\leq 2$
b.
$f'(x)=x^2-3x+2=0$
$\Leftrightarrow 3x^2-6x=x^2-3x+2=0$
$\Leftrightarrow 3x(x-2)=(x-1)(x-2)=0$
$\Leftrightarrow x-2=0$
$\Leftrightarrow x=2$
c.
$g(x)=f(1-2x)+x^2-x+2022$
$g'(x)=(1-2x)'f(1-2x)'_{1-2x}+2x-1$
$=-2[3(1-2x)^2-6(1-2x)]+2x-1$
$=-24x^2+2x+5$
$g'(x)\geq 0$
$\Leftrightarrow -24x^2+2x+5\geq 0$
$\Leftrightarrow (5-12x)(2x-1)\geq 0$
$\Leftrightarrow \frac{-5}{12}\leq x\leq \frac{1}{2}$

\(a,0,1^{2-x}>0,1^{4+2x}\\ \Leftrightarrow2-x>2x+4\\ \Leftrightarrow3x< -2\\ \Leftrightarrow x< -\dfrac{2}{3}\)
\(b,2\cdot5^{2x+1}\le3\\ \Leftrightarrow5^{2x+1}\le\dfrac{3}{2}\\ \Leftrightarrow2x+1\le log_5\left(\dfrac{3}{2}\right)\\ \Leftrightarrow2x\le log_5\left(\dfrac{3}{2}\right)-1\\ \Leftrightarrow x\le\dfrac{1}{2}log_5\left(\dfrac{3}{2}\right)-\dfrac{1}{2}\\ \Leftrightarrow x\le log_5\left(\dfrac{\sqrt{30}}{10}\right)\)
c, ĐK: \(x>-7\)
\(log_3\left(x+7\right)\ge-1\\ \Leftrightarrow x+7\ge\dfrac{1}{3}\\ \Leftrightarrow x\ge-\dfrac{20}{3}\)
Kết hợp với ĐKXĐ, ta có:\(x\ge-\dfrac{20}{3}\)
d, ĐK: \(x>\dfrac{1}{2}\)
\(log_{0,5}\left(x+7\right)\ge log_{0,5}\left(2x-1\right)\\ \Leftrightarrow x+7\le2x-1\\ \Leftrightarrow x\ge8\)
Kết hợp với ĐKXĐ, ta được: \(x\ge8\)

Chọn A
Ta có: f ' ( x ) = 6 x 2 − 6 x
Để
f ' ( x ) ≥ 0 ⇔ 6 x 2 − 6 x ≥ 0 ⇔ x ≤ 0 x ≥ 1

2: ĐKXĐ: x<>1
\(f'\left(x\right)=\dfrac{\left(x^2-3x+3\right)'\left(x-1\right)-\left(x^2-3x+3\right)\left(x-1\right)'}{\left(x-1\right)^2}\)
\(=\dfrac{\left(2x-3\right)\left(x-1\right)-\left(x^2-3x+3\right)}{\left(x-1\right)^2}\)
\(=\dfrac{2x^2-5x+3-x^2+3x-3}{\left(x-1\right)^2}=\dfrac{x^2-2x}{\left(x-1\right)^2}\)
f'(x)=0
=>x^2-2x=0
=>x(x-2)=0
=>\(\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)
1:
\(f\left(x\right)=\dfrac{1}{3}x^3-2\sqrt{2}\cdot x^2+8x-1\)
=>\(f'\left(x\right)=\dfrac{1}{3}\cdot3x^2-2\sqrt{2}\cdot2x+8=x^2-4\sqrt{2}\cdot x+8=\left(x-2\sqrt{2}\right)^2\)
f'(x)=0
=>\(\left(x-2\sqrt{2}\right)^2=0\)
=>\(x-2\sqrt{2}=0\)
=>\(x=2\sqrt{2}\)
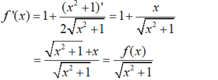
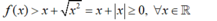
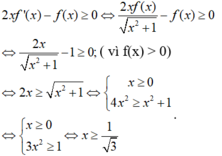
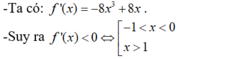
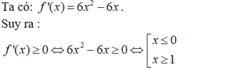
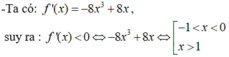
x < 1 hoặc x > 2