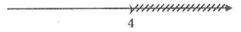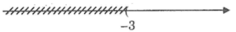YL
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PT
1
CM
12 tháng 10 2017
3x + 4 < 0
⇔ 3x < -4 (chuyển vế 4).
⇔ 
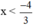(Chia cả hai vế cho 3 > 0).
Vậy BPT có tập nghiệm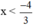 
PT
1
CM
6 tháng 11 2017
4 – 3x ≤ 0
⇔ -3x ≤ -4 (Chuyển vế hạng tử 4).
⇔ 
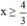(Chia cả hai vế cho -3 < 0, BPT đổi chiều).
Vậy BPT có tập nghiệm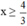 
PT
1
PT
1
27 tháng 6 2016
\(x^2-4x+3\ge0\)
\(\left(x-1\right)\left(x-3\right)\ge0\)
TH1; X-1>=0 VA X-3>=0
TH2: X-1=<0 VA X-3<=0
Vay x>=3 hoac x<=1
KV
29 tháng 4 2022
Ta có:
\(-2018m>-2018n\)
\(\Rightarrow-2018m.\left(-\dfrac{1}{2018}\right)< -2018n.\left(-\dfrac{1}{2018}\right)\)
\(\Rightarrow m>n\)
b) \(x^2-x\left(x+2\right)>3x-1\)
\(\Leftrightarrow x^2-x^2-2x>3x-1\)
\(\Leftrightarrow-2x-3x>-1\)
\(\Leftrightarrow-5x>-1\)
\(\Leftrightarrow x< \dfrac{1}{5}\)
Vậy S = {\(x\) | \(x< \dfrac{1}{5}\)}
29 tháng 4 2022
a) Ta có: -2018m > -2018n
\(\Leftrightarrow-2018m\times\left(\dfrac{-1}{2018}\right)< -2018n\times\left(\dfrac{-1}{2018}\right)\)
\(\Leftrightarrow\) m < n
DD
27 tháng 4 2019
x + x - 1/2 > x - 2/3
<=> 2x - 1/2 > x - 2/3
<=> x > -1/6
x/3 + 3x - 4/5 >= 2x - 3
<=> 4x/3 >= -11/5
<=> 4x >= -33/5
<=> x >= -33/20
Tập nghiệm chung của 2 bất phương trình là : x >-1/6
ND
25 tháng 4 2018
a) \(x^2-4x+3\ge0\)
\(\Leftrightarrow x^2-3x-x+3\ge0\)
\(\Leftrightarrow x\left(x-3\right)-\left(x-3\right)\ge0\)
\(\Leftrightarrow\left(x-3\right)\left(x-1\right)\ge0\)
* \(x-3\ge0\) và \(x-1\ge0\)
\(\Leftrightarrow x\ge3\) và \(x\ge1\)
\(\Leftrightarrow x\ge3\)
* \(x-3\le0\) và \(x-1\le0\)
\(\Leftrightarrow x\le3\) và \(x\le1\)
\(\Leftrightarrow x\le1\)
Vậy \(x\ge3\) và \(x\le1\)
26 tháng 4 2018
b) x3 - 2x2 + 3x - 6 < 0
⇔ x2( x - 2 ) + 3( x - 2) < 0
⇔ ( x - 2)( x2 + 3) < 0
Do : x2 + 3 > 0 ∀x
⇒ x - 2 < 0
⇒ x < 2
KL....