OLM cung cấp gói bải giảng điện tử PPT cho giáo viên đầu năm học

Thi thử và xem hướng dẫn giải chi tiết đề tham khảo 12 môn thi Tốt nghiệp THPT 2025

Tập huấn miễn phí ra đề kiểm tra và chấm phiếu trắc nghiệm dành cho giáo viên khối THCS

K
Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
Mua vip
PT
Pham Trong Bach
22 tháng 4 2018

Giải bất phương trình log 2 ( 3 x - 2 )   >   log 2 ( 6 - 5 x )   được tập nghiệm là (a;b). Hãy tính tổng S=a+b 

A.  S = 8 3

B.  S = 28 15

C.  S = 11 5

D.  S = 31 6

#Mẫu giáo
1
CM
Cao Minh Tâm
22 tháng 4 2018

Đúng(0)
PT
Pham Trong Bach
7 tháng 12 2017
Giải bất phương trình log 2 3 x - 2 > log 2 6 - 5 x  được tập nghiệm là (a;b).Hãy tính tổng S=a+b A.  8/5 B.  28/15 C.  11/5 D....
Đọc tiếp

Giải bất phương trình log 2 3 x - 2 > log 2 6 - 5 x  được tập nghiệm là (a;b).Hãy tính tổng S=a+b

A.  8/5

B.  28/15

C.  11/5

D.  26/5
#Mẫu giáo
1
CM
Cao Minh Tâm
7 tháng 12 2017

Đáp án C

Đúng(0)
PT
Pham Trong Bach
12 tháng 4 2017
Gọi S là tập  nghiệm  của  bất phương trình 2 x 3 + x ≤ x + 2 2 x + 5 .   Biết S = a ; b , a , b ∈ ℝ .  Giá trị M = a 2 b 3  của gần nhất với số nào sau đây: A. 0,12 B. 2,42 C. 2,12 D....
Đọc tiếp

Gọi S là tập  nghiệm  của  bất phương trình 2 x 3 + x ≤ x + 2 2 x + 5 .   Biết S = a ; b , a , b ∈ ℝ .  Giá trị M = a 2 b 3  của gần nhất với số nào sau đây:

A. 0,12

B. 2,42

C. 2,12

D. 1,12
#Mẫu giáo
1
CM
Cao Minh Tâm
12 tháng 4 2017

Đáp án C

Đúng(0)
PT
Pham Trong Bach
12 tháng 12 2019
Bất phương trình 2 log 9 x + 2 − log 3 1 − x ≥ 1 có tập nghiệm là S = [ a ; b ) .  Tính P = 4 a + 1 2 + b 3 . A.  P = − 1. B.  P = 5. C.  P = 4. D.  P = 1. ...
Đọc tiếp

Bất phương trình 2 log 9 x + 2 − log 3 1 − x ≥ 1 có tập nghiệm là S = [ a ; b ) .  Tính P = 4 a + 1 2 + b 3 .

A.  P = − 1.

B.  P = 5.

C.  P = 4.

D.  P = 1.

#Mẫu giáo
1
CM
Cao Minh Tâm
12 tháng 12 2019

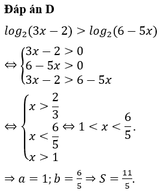
Đáp án B.                                             

TXĐ:  x + 2 > 0 1 − x > 0 ⇔ − 2 < x < 1.

Bất phương trình tương đương với: 

log 3 x + 2 1 − x ≥ 1 ⇔ x + 2 1 − x ≥ 3 ⇔ x + 2 ≥ 3 − 3 x ⇔ x ≥ 1 4 .

Do đó  a = 1 4 ; b = 1  nên 

S = 2 2 + 1 3 = 5.

Đúng(0)
PT
Pham Trong Bach
8 tháng 2 2018
Biết rằng tập nghiệm S của bất phương trình log - x 2 + 100 x - 2400 < 2  có dạng S = a ; b \ x ∘ . Giá trị của a + b - x ∘  bằng: A. 150. B. 100. C. 30....
Đọc tiếp

Biết rằng tập nghiệm S của bất phương trình log - x 2 + 100 x - 2400 < 2  có dạng S = a ; b \ x ∘ . Giá trị của a + b - x ∘  bằng:

A. 150.

B. 100.

C. 30.

D. 50.
#Mẫu giáo
1
CM
Cao Minh Tâm
8 tháng 2 2018

Đáp án D

Đúng(0)
PT
Pham Trong Bach
8 tháng 3 2017

Biết tập nghiệm S của bất phương trình  log π 6 log 3 x - 2 > 0  là khoảng (a;b). Tính b - a.

A. 2

B. 4

C. 3

D. 5
#Mẫu giáo
1
CM
Cao Minh Tâm
8 tháng 3 2017

Đáp án A.

Ta có:   log π 6 log 3 x - 2 > 0 ⇔ 0 < log 3 x - 2 < 1 ⇔ x - 2 > 1 x - 2 < 3 ⇔ 3 < x < 5

Vậy S = 3 ; 5 ⇒ b - a = 2 .

Đúng(0)
PT
Pham Trong Bach
30 tháng 3 2017
Gọi S là tập tất cả các giá trị thực của tham số m để bất phương trình x 6 + 3 x 4 − m 3 x 3 + 4 x 2 − m x + 2 ≥ 0  có nghiệm  với  mọi x ∈ ℝ .  Biết  rằng S = a ; b , a , b ∈ ℝ .  Tính  P = 2 b − 3 a A. P = 5 B. P = 10 C. P = 15 D. P =...
Đọc tiếp

Gọi S là tập tất cả các giá trị thực của tham số m để bất phương trình

x 6 + 3 x 4 − m 3 x 3 + 4 x 2 − m x + 2 ≥ 0  có nghiệm  với  mọi x ∈ ℝ .  Biết  rằng S = a ; b , a , b ∈ ℝ .  Tính  P = 2 b − 3 a

A. P = 5

B. P = 10

C. P = 15

D. P = 0
#Mẫu giáo
1
CM
Cao Minh Tâm
30 tháng 3 2017

Chọn B

Đúng(0)
PT
Pham Trong Bach
16 tháng 4 2018

Tập nghiệm của bất phương trình log 2 x - log x 3 + 2 ≥ 0  là S = ( a ; b ] ∪ [ c ; + ∞ )  thì a + b + c là:

A. 10

B. 100

C. 110

D. 2018
#Mẫu giáo
1
CM
Cao Minh Tâm
16 tháng 4 2018

Đáp án C

Đúng(0)
PT
Pham Trong Bach
22 tháng 5 2019
Biết rằng bất phương trình log 2 5 x + 2 + 2 . log 5 x + 2 2 > 3  có tập nghiệm là S = log a b ; + ∞ , với a, b là các số nguyên dương nhỏ hơn 6 và a ≠ 1  . Tính P = 2 a + 3 b . A.  P = 7                    B.  P = 11 C.  P = ...
Đọc tiếp

Biết rằng bất phương trình log 2 5 x + 2 + 2 . log 5 x + 2 2 > 3  có tập nghiệm là S = log a b ; + ∞ , với a, b là các số nguyên dương nhỏ hơn 6 và a ≠ 1  . Tính P = 2 a + 3 b .

A.  P = 7                   

B.  P = 11

C.  P = 18

D.  P = 16

#Mẫu giáo
1
CM
Cao Minh Tâm
22 tháng 5 2019

Ta có:

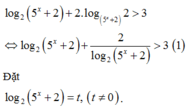
Ta có

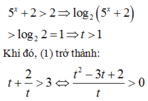
Ta có bảng xét dấu sau:

 

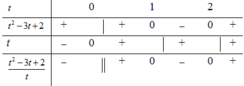
Từ BBT kết hợp điều kiện của t ta có:

Chọn: D

Đúng(0)
Bảng xếp hạng
Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
  • Tuần
  • Tháng
  • Năm
Các khóa học có thể bạn quan tâm
Tổng thanh toán: 0đ (Tiết kiệm: 0đ)
Tới giỏ hàng
Yêu cầu VIP