Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ĐKXĐ: ...
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{3}{x+y}+6x-3y=6\\\dfrac{3}{x+y}+2x-4y=1\end{matrix}\right.\)
\(\Rightarrow4x+y=5\Rightarrow y=5-4x\)
Thế vào phương trình đầu:
\(\dfrac{1}{x+5-4x}+2x-\left(5-4x\right)=2\)
\(\Leftrightarrow\dfrac{1}{5-3x}+6x-7=0\)
\(\Leftrightarrow\left(6x-7\right)\left(5-3x\right)+1=0\)
\(\Leftrightarrow...\)

\(\dfrac{x-2}{x+1}-\dfrac{3}{x+2}>0.\left(x\ne-1;-2\right).\\ \Leftrightarrow\dfrac{x^2-4-3x-3}{\left(x+1\right)\left(x+2\right)}>0.\\ \Leftrightarrow\dfrac{x^2-3x-7}{\left(x+1\right)\left(x+2\right)}>0.\)
Đặt \(f\left(x\right)=\dfrac{x^2-3x-7}{\left(x+1\right)\left(x+2\right)}>0.\)
Ta có: \(x^2-3x-7=0.\Rightarrow\left[{}\begin{matrix}x=\dfrac{3+\sqrt{37}}{2}.\\x=\dfrac{3-\sqrt{37}}{2}.\end{matrix}\right.\)
\(x+1=0.\Leftrightarrow x=-1.\\ x+2=0.\Leftrightarrow x=-2.\)
Bảng xét dấu:
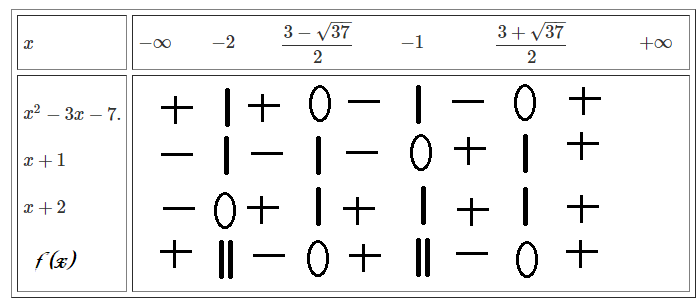
\(\Rightarrow f\left(x\right)>0\Leftrightarrow x\in\left(-\infty-2\right)\cup\left(\dfrac{3-\sqrt{37}}{2};-1\right)\cup\left(\dfrac{3+\sqrt{37}}{2};+\infty\right).\)
\(\sqrt{x^2-3x+2}\ge3.\\ \Leftrightarrow x^2-3x+2\ge9.\\ \Leftrightarrow x^2-3x-7\ge0.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{3-\sqrt{37}}{2}.\\x=\dfrac{3+\sqrt{37}}{2}.\end{matrix}\right.\)
Đặt \(f\left(x\right)=x^2-3x-7.\)
\(f\left(x\right)=x^2-3x-7.\)
\(\Rightarrow f\left(x\right)\ge0\Leftrightarrow x\in(-\infty;\dfrac{3-\sqrt{37}}{2}]\cup[\dfrac{3+\sqrt{37}}{2};+\infty).\)
\(\Rightarrow\sqrt{x^2-3x+2}\ge3\Leftrightarrow x\in(-\infty;\dfrac{3-\sqrt{37}}{2}]\cup[\dfrac{3+\sqrt{37}}{2};+\infty).\)

Đặt \(f\left(x\right)=\dfrac{x-1}{\left(x-2\right)\left(x-3\right)}.\)
\(x-1=0.\Leftrightarrow x=1.\\ x-2=0.\Leftrightarrow x=2.\\ x-3=0.\Leftrightarrow x=3.\)
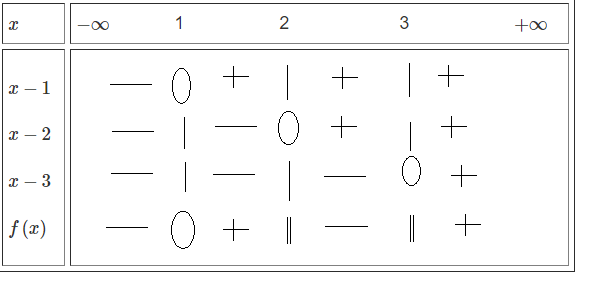
\(\Rightarrow f\left(x\right)>0\Leftrightarrow x\in\) \(\left(1;2\right)\cup\left(3;+\infty\right).\)
\(\Rightarrow B.\)

a.
Do K thuộc d nên tọa độ có dạng: \(K\left(a;2-a\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AK}=\left(a-3;-a-2\right)\\\overrightarrow{BK}=\left(a-2;1-a\right)\\\overrightarrow{CK}=\left(a+1;4-a\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}AK^2=\left(a-3\right)^2+\left(-a-2\right)^2=2a^2-2a+13\\BK^2=\left(a-2\right)^2+\left(1-a\right)^2=2a^2-6a+5\\CK^2=\left(a+1\right)^2+\left(4-a\right)^2=2a^2-6a+17\end{matrix}\right.\)
\(T=AK^2-2BK^2-CK^2=2a^2-2a+13-2\left(2a^2-6a+5\right)-\left(2a^2-6a+17\right)\)
\(=-4a^2+16a-14=-4\left(a-2\right)^2+2\le2\)
Dấu "=" xảy ra khi \(a=2\Rightarrow K\left(2;0\right)\)
b. Điểm M là điểm nào nhỉ?

Bài 1:
Khai bút đầu năm lấy may :''>
Đặt $x^2+ax+1=t$ thì ta có hệ \(\left\{\begin{matrix} x^2+ax+(1-t)=0(1)\\ t^2+at+1=0(2)\end{matrix}\right.\)
Trước tiên, pt $(2)$ cần có nghiệm.
Điều này xảy ra khi $\Delta_{(2)}=a^2-4\geq 0\Leftrightarrow a\geq 2$ hoặc $a\leq -2$
Để PT ban đầu có nghiệm duy nhất thì PT $(1)$ phải có nghiệm duy nhất. Điều này xảy ra khi $\Delta_{(1)}=a^2-4(1-t)=0$
$\Leftrightarrow 4(1-t)=a^2$. Mà $a^2\geq 4$ nên $1-t\geq 1\Rightarrow t\leq 0$
------------------
Giờ ta xét:
Nếu $a\leq -2$. Kết hợp với $t\leq 0\Rightarrow at\geq -2t$
$\Rightarrow 0=t^2+at+2\geq t^2-2t+1\Leftrightarrow 0\geq (t-1)^2$.
$\Rightarrow t-1=0\Rightarrow t=1$ (vô lý vì $t\leq 0$)
Do đó $a\geq 2$
Tuy nhiên thay $a=2$ vào hệ ta thấy không thỏa mãn. Do đó $a>2$ (đpcm)
Bài 2:
Nếu $a=0\Rightarrow 2b+5c=0\Rightarow c=\frac{-2}{5}b$
PT trở thành: $bx+c=0$
$\Leftrightarrow bx-\frac{2}{5}b=0$ có nghiệm duy nhất $x=\frac{2}{5}$ nếu $b\neq 0$ hoặc vô số nghiệm nếu $b=0$
Tức là với $a=0$ pt luôn có nghiệm.
Nếu $a\neq 0$. PT đã cho là pt bậc hai ẩn $x$
Xét $\Delta=b^2-4ac=b^2-4(-2b-5c)c=b^2+8bc+20c^2=(b+4c)^2+4c^2\geq 0$ với mọi $b,c$ nên PT đã cho luôn có nghiệm.
Vậy........

Hàm xác định trên R
\(f\left(-x\right)=\dfrac{\left|-x+1\right|-\left|-x-1\right|}{\left|-x+2\right|+\left|-x-2\right|}=\dfrac{\left|x-1\right|-\left|x+1\right|}{\left|x+2\right|+\left|x-2\right|}=-f\left(x\right)\)
Hàm đã cho là hàm lẻ
\(\dfrac{-x^2-3x+18}{\left(x-2\right)\left(x+2\right)}< 0\)
\(\Leftrightarrow\dfrac{x^2+3x-18}{\left(x-2\right)\left(x+2\right)}>0\)
Theo BXD, ta có: f(x)>0
=>\(x\in\left(-\infty;-6\right)\cup\left(-2;2\right)\cup\left(3;+\infty\right)\)