
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

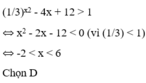

g'(x) là đạo hàm của g(x) phải không bạn? Xét đạo hàm tới 2 lần lận à?


Lời giải:
Đồ thị màu xanh lá là $y=4^x$
Đồ thị màu xanh dương là $y=\left(\frac{1}{4}\right)^x$


câu 1 sao không ra đáp án nào vậy bạn , hình như bạn làm sai đâu đó rồi
Trời, đọc xong chỉ việc chọn đáp án mà ko biết chọn luôn?
Đáp án D chứ sao nữa

19.
\(\overline{z}=1-3i\)
\(\Rightarrow u=\left(1-3i\right)\left(2-i\right)=2+3i^2-7i=-1-7i\)
Phần ảo bằng -7
20.
Tọa độ G: \(\left\{{}\begin{matrix}x_G=\frac{x_A+x_B+x_C}{3}=2\\y_G=\frac{y_A+y_B+y_C}{3}=1\end{matrix}\right.\)
Biểu diễn trên mặt phẳng phức: \(z=2+i\)
21.
Đề đúng là \(\left(1-i\right)+44\overline{z}=7-7i\) chứ?
\(\Rightarrow44\overline{z}=6-6i\Rightarrow\overline{z}=\frac{3}{22}-\frac{3}{22}i\)
\(\Rightarrow z=\frac{3}{22}+\frac{3}{22}i\Rightarrow\left|z\right|=\sqrt{\left(\frac{3}{22}\right)^2+\left(\frac{3}{22}\right)^2}=\frac{3\sqrt{2}}{22}\)
15.
Diện tích thiết diện:
\(S=\frac{1}{2}\left(2\sqrt{1-x^2}\right)^2=2\left(1-x^2\right)=2-2x^2\)
Thể tích:
\(S=\int\limits^1_{-1}\left(2-2x^2\right)dx=\frac{8}{3}\)
16.
\(z=z'\Leftrightarrow\left\{{}\begin{matrix}a=c\\b=d\end{matrix}\right.\) (phần thực bằng phần thực, phần ảo bằng phần ảo)
17.
\(\overline{z}=3+2i\Rightarrow\) phần ảo là 2 (không phải 2i đâu)
18.
\(z=3+2i\Rightarrow z^2=\left(3+2i\right)^2=9+4i^2+12i=5+12i\)
\(\Rightarrow\) phần thực bằng 5

a) Xét hàm số y = f(x) = tanx – x với x ∈ [0 ; ).
Ta có : y’ = - 1 ≥ 0, x ∈ [0 ;
); y’ = 0 ⇔ x = 0. Vậy hàm số luôn đồng biến trên [0 ;
).
Từ đó ∀x ∈ (0 ; ) thì f(x) > f(0) ⇔ tanx – x > tan0 – 0 = 0 hay tanx > x.
b) Xét hàm số y = g(x) = tanx – x - . với x ∈ [0 ;
).
Ta có : y’ = - 1 - x2 = 1 + tan2x - 1 - x2 = tan2x - x2
= (tanx - x)(tanx + x), ∀x ∈ [0 ; ).
Vì ∀x ∈ [0 ; ) nên tanx + x ≥ 0 và tanx - x >0 (theo câu a).
Do đó y' ≥ 0, ∀x ∈ [0 ; ).
Dễ thấy y' = 0 ⇔ x = 0. Vậy hàm số luôn đồng biến trên [0 ; ). Từ đó : ∀x ∈ [0 ;
) thì g(x) > g(0) ⇔ tanx – x -
> tan0 - 0 - 0 = 0 hay tanx > x +
.

tìm 2 điểm A và B . tam giác vuông tại 0 => vecto OA*OB= 0 với O là gốc
a đù xem lần đầu sao k có pt h lại có . bài này mk tìm dc denta'=1=> nghiệm x1=m+1:x2=m-1( theo công thức nghiệm)=>A(m+1:0),B(m-1;0) => vì tam giác OAB vuông mà O là gốc nên => tích OA.OB=0 <=>(m+1)*(m-1)+0*0=0 => m^2-1=0 => m=+-1