Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có: Vận tốc đầu ở đỉnh dốc = 0 ( v0= 0) quả cầu chuyển động nhanh dần đều
S = 0 + (1/2).a.t²
=> a = 2.S/t²
= 2.100/10²
= 2 m/s²
ta có:
- Quả cầu nằm ngang trên mặt phẳng và chuyển động chậm dần với gia tốc a'
- Tốc độ đầu v là tốc độ tại chân dốc, tốc độ cuối = 0
v = 0 + a.t
= 0 + 2.10
= 20 (m/s)
Ta lại có: 0² - v² = 2.a'S
=> a' = -v²/2S
= - 20²/2.50
= - 4 (m/s²) ( vật chuyển động chậm dần đều )
b) Thời gian mà vật chuyển động trên mặt phẳng ngang t' là:
0 = v - a't'
=> t' = v/a' = 20/4 = 5 (s)
Thời gian quả cầu chuyển động trong cả quá trình là:
t + t' = 10 + 5 = 15 (s)
a)* Từ đỉnh dốc vận tốc đầu = 0, quả cầu chuyển động nhanh dần
S = 0 + (1/2)at²
=> a = 2S/t² = 2*100/10² = 2 m/s²
*Trên mặt phẳng ngang quả cầu chuyển động chậm dần với gia tốc a', tốc độ đầu v là tốc độ tại chân dốc, tốc độ cuối = 0
v = 0+at = 0 + 2.10 = 20 m/s
Có: 0² - v² = 2.a'S
=> a' = -v²/2S = -20²/2.50 = -4 (m/s²) (dấu - chứng tỏ vật cđộng chậm dần)
b) thời gian chuyển động trên mặt phẳng ngang: t'
0 = v - a't' => t' = v/a' = 20/4 = 5s
thời gian của cả quá trình chuyển động: t + t' = 10 + 5 = 15s
Chúc bạn học tốt !!!

Tham khảo:
a)
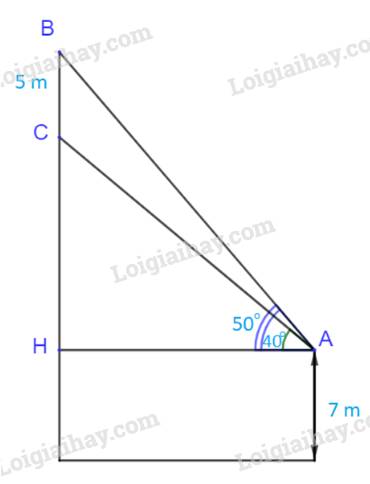
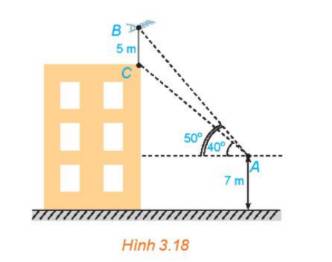
Gọi H là hình chiếu của A lên đường thẳng BC.
Ta có: \(\widehat {HAB} = {50^o}\); \(\widehat {HAC} = {40^o}\)
\( \Rightarrow \widehat {BAC} = {50^o} - {40^o} = {10^o}\) (1)
Xét tam giác ABH, vuông tại H ta có:
\(\widehat H = {90^o};\;\widehat {BAH} = {50^o}.\)
\( \Rightarrow \widehat {HBA} = {180^o} - {90^o} - {50^o} = {40^o}\) hay \(\widehat {CBA} = {40^o}\). (2)
Từ (1) và (2), suy ra: \(\widehat {BCA} = {180^o} - {40^o} - {10^o} = {130^o}.\)
Vậy ba góc của tam giác ABC lần lượt là: \(\widehat A = {10^o};\;\widehat B = {40^o};\;\widehat C = {130^o}\).
b)
Áp dụng định lý sin cho tam giác ABC, ta được:
\(\frac{{BC}}{{\sin A}} = \frac{{AC}}{{\sin B}} = \frac{{AB}}{{\sin C}}\) \( \Rightarrow AB = \frac{{BC.\sin C}}{{\sin A}}\)
Mà: \(BC = 5\;(m);\;\;\widehat C = {130^o};\;\widehat A = {10^o}\)
\( \Rightarrow AB = \frac{{5.\sin {{130}^o}}}{{\sin {{10}^o}}} \approx 22\;(m)\)
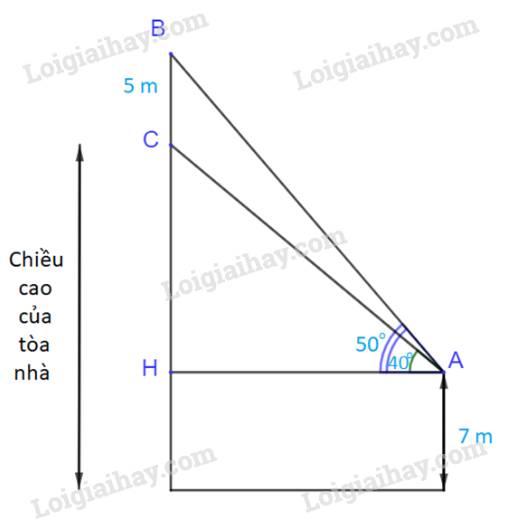
Xét tam giác ABH, vuông tại H ta có:
\(\sin \widehat {BAH} = \frac{{BH}}{{AB}}\)\( \Rightarrow BH = AB.\,\,\sin \widehat {BAH}\)
Mà: \(AB \approx 22\;(m);\;\;\widehat {BAH} = {50^o}\)
\( \Rightarrow BH \approx 22.\sin {50^o} \approx 16,85\;(m)\)
Vậy chiều cao của tòa nhà là: \(BH-{\rm{ }}BC + 7 = 16,85-5 + 7 = 18,85{\rm{ }}\left( m \right)\)

ve hinh thang vuong ABED co AD//BC ; va ED vuong goc voi BC keo dai ;
E thuoc BC keo dai(hinh chieu cua BC tren mat dat)
.D la diem duoi mat dat cua A AD=7m; BC=5m
Cac goc 40 ; 50 do la giua AC ; AB voi phuong nam ngang .
Ta tinh duoc DE theo BC : DE =BC/(tan50-tan40)
=> Bc da biet tan ta tra duoc .Con CE la chieu cao cua nha :
Vay : CE=AD+DE*tan40= 7+5*tan40/(tan50-tan40)

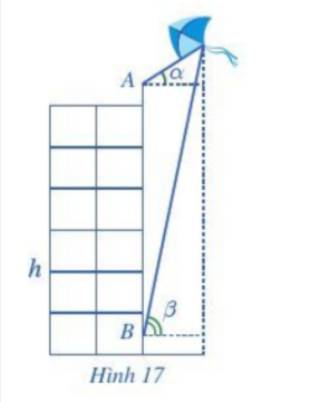
Gọi các điểm:
O là vị trí của chiếc diều.
H là hình chiếu vuông góc của chiếc diều trên mặt đất.
C, D lần lượt là hình chiếu vuông góc của A, B trên OH.
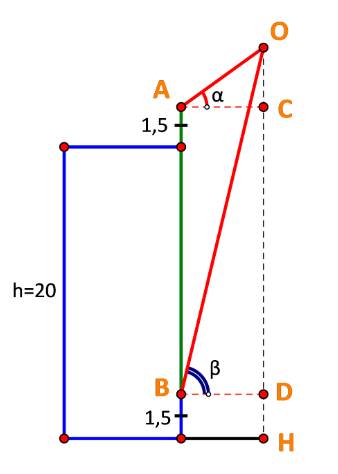
Đặt OC = x, suy ra OH = x + 20 + 1,5 =x + 21,5.
Xét tam giác OAC, ta có: \(\tan \alpha = \frac{{OC}}{{AC}} \Rightarrow AC = \frac{{OC}}{{\tan \alpha }} = \frac{x}{{\tan {{35}^o}}}\)
Xét tam giác OBD, ta có: \(\tan \beta = \frac{{OD}}{{BD}} \Rightarrow BD = \frac{{OD}}{{\tan \beta }} = \frac{{x + 20}}{{\tan {{75}^o}}}\)
Mà:\(AC = BD\)\( \Rightarrow \frac{x}{{\tan {{35}^o}}} = \frac{{x + 20}}{{\tan {{75}^o}}}\)
\(\begin{array}{l} \Leftrightarrow x.\tan {75^o} = \left( {x + 20} \right).\tan {35^o}\\ \Leftrightarrow x = \frac{{20.\tan {{35}^o}}}{{\tan {{75}^o} - \tan {{35}^o}}} \approx 4,6\end{array}\)
Suy ra OH = 26,1.
Vậy chiếc diều bay cao 26,1 m so với mặt đất.