Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giải thích các bước giải:
Gọi số dãy ghế ban đầu là x (dãy) (x>0)
=> số ghế của 1 dãy ban đầu là 120/x (ghế)
Khi kê thì kê được: x+2 (dãy) và số ghế 1 dãy là: 120/(x+2)
Ta có phương trình:
120x−120x+2=2⇒1x−1x+2=2120⇒x+2−xx(x+2)=160⇒60.2=x2+2x⇒x2+2x−120=0⇒x=10(do:x>0)120x−120x+2=2⇒1x−1x+2=2120⇒x+2−xx(x+2)=160⇒60.2=x2+2x⇒x2+2x−120=0⇒x=10(do:x>0)
Vậy trước khi sửa thì rạp có 10 dãy ghế.

Gọi số dãy ghế có trong phòng họp lúc đầu là x (x<50)
Lúc đầu mỗi dãy có \(\frac{240}{x}\)ghế
Vì lúc sau có 315 người tham dự nên phải kê thêm 3 dãy, mỗi dãy thêm 1 ghế
=> \(\left(\frac{240}{x}+1\right)\left(x+3\right)=315\Leftrightarrow240+\frac{720}{x}+x+3=315\)
\(\Leftrightarrow x-72+\frac{720}{x}=0\Leftrightarrow\frac{x^2-72x+720}{x}=0\Leftrightarrow x^2-72x+720=0\)
\(\Delta'=\left(-36\right)^2-720=576\)
=> x1= 60 (Loại), x2=12 (thỏa mãn)
Vậy trong phòng họp lúc đầu có 12 dãy ghế.

bài mẫu nè:
gọi số dãy ghế là x, số ghê là y
theo đb ta có hpt
(x-2)(y+2)=288
xy=288
giải pt tìm đk x=18; y=16

Gọi số ghế ở mỗi hàng ban đầu là x (ghế, x > 0)
Gọi số hàng ghế trong phòng ban đầu là y (hàng, y < 50)
Ta có x nhân y = 240
Khi tăng số ghế và số hàng ta có (x + 1)(y + 3)= 315
Ta có hệ phương trình {x nhân y= 240
{y + 3x = 72
Giải hệ phương trình ta có y= 12; x= 20
Vậy số dãy ghế có trong phòng lúc đầu là 12 hàng.

gọi số hàng ghế ban đầu là x ( hàng )( đk x>0)
\(\Rightarrow\)số hàng ghế sau khi thêm một hàng là x+1 ( hàng)
số ghế trên một hàng ban đầu là \(\frac{300}{x}\)(ghế)
số ghế trên một hàng sau khi thêm hai ghế và một hàng là \(\frac{357}{x+1}\)(ghế)
ta có phương trình : \(\frac{357}{x+1}\)=\(\frac{300}{x}\)+2
\(\Rightarrow\)357x =300x+300 +2x\(^2\)+2
\(\Leftrightarrow\)-2x\(^2\)+57x-302=0
\(\Leftrightarrow\)2x\(^2\)-57x+302=0
giải phương trình bậc hai
đối chiếu điều kiện
kết luận

gọi x và y lần lượt là số dãy ghs và số ghế trong một dãy
Do đó x,y là hai số tự nhiên khác 0
ta có hệ sau
\(\hept{\begin{cases}x.y=320\\\left(x+1\right)\left(y+4\right)=420\end{cases}\Leftrightarrow}\hept{\begin{cases}x.y=320\\xy+4x+y+4=420\end{cases}\Leftrightarrow\hept{\begin{cases}x.y=320\\4x+y=96\end{cases}}}\)
Rút \(y=96-4x\Rightarrow96x-4x^2=320\Leftrightarrow\orbr{\begin{cases}x=20\Rightarrow y=16\\x=4\Rightarrow y=40\end{cases}}\)
Vậy có hai khả năng xảy ra như trên

Gọi số dãy ghế có trong phòng họp lúc đầu là x (x<50)
Lúc đầu mỗi dãy có ghế
Vì lúc sau có 315 người tham dự nên phải kê thêm 3 dãy, mỗi dãy thêm 1 ghế
=>
=> x1= 60 (Loại), x2=12 (thỏa mãn)
Vậy trong phòng họp lúc đầu có 12 dãy ghế.

Gọi số dãy ghế lúc ban đầu là x(dãy)
(Điều kiện: \(x\in Z^+\))
Số người ngồi trên 1 dãy ghế ban đầu là \(\dfrac{80}{x}\left(người\right)\)
Số dãy ghế khi bớt đi 2 dãy là x-2(dãy)
Số người ngồi trên 1 dãy ghế khi bớt đi 2 dãy ghế là \(\dfrac{80}{x-2}\left(người\right)\)
Theo đề, ta có phương trình:
\(\dfrac{80}{x-2}-\dfrac{80}{x}=2\)
=>\(\dfrac{80x-80\left(x-2\right)}{x\left(x-2\right)}=2\)
=>\(\dfrac{160}{x\left(x-2\right)}=2\)
=>x(x-2)=80
=>\(x^2-2x-80=0\)
=>(x-10)(x+8)=0
=>\(\left[{}\begin{matrix}x-10=0\\x+8=0\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=10\left(nhận\right)\\x=-8\left(loại\right)\end{matrix}\right.\)
Vậy: Số dãy ghế ban đầu là 10 dãy
Số người ngồi trên 1 dãy ban đầu là 80:10=8 người

Gọi số dãy ghế là x (x ∈ ℕ * ), (dãy)
Số ghế ở mỗi dãy là: 360/x (ghế)
Số dãy ghế lúc sau là x + 1 (dãy)
Số ghế ở mỗi dãy lúc sau là: 360/x + 1(ghế)
Vì sau khi tăng số dãy thêm 1 và số ghế của mỗi dãy tăng thêm 1 thì trong phòng có 400 ghế nên ta có phương trình:
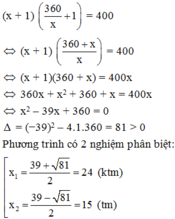
Vậy số dãy ghế là 15 (dãy)
Đáp án: B
Gọi số ghế là dãy ghế là x
số ghế trong 1 dãy là y
+) \(\hept{\begin{cases}x.y=120\\\left(x+2\right).\left(y-2\right)=120\end{cases}\left(x,y>0\right)}\)
+)\(\hept{\begin{cases}x.y=120\\x.y+2.y-2.x-4=120\end{cases}}\)
+) 2.y - 2.x = 4 <=> y- x = 2
=> y = x + 2
=> x . ( x + 2 ) =120
<=> x2 + 2.x - 120 = 0
<=> \(\orbr{\begin{cases}x=10\\x=-12\left(L\right)\end{cases}}\)=> ta có 10 dãy
=> y = 12