NN
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HQ
Hà Quang Minh
Giáo viên
1 tháng 10 2023
Số cách sắp xếp 6 vận động viên vào 6 đường chạy là số hoán vị của 6 phần tử.
=> Số cách xếp các vận động viên vào các đường chạy đó là:
6! = 720 cách
HQ
Hà Quang Minh
Giáo viên
30 tháng 9 2023
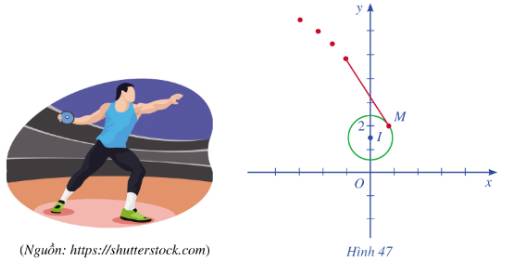
Sau khi được ném đi, quỹ đạo chuyển động của chiếc đĩa nằm trên tiếp tuyến của đường tròn tâm I tại điểm M.
Vậy quỹ đạo chuyển động của chiếc đĩa nằm trên đường thẳng có phương trình là:
\(\begin{array}{l}\left( {\frac{{\sqrt {39} }}{{10}} - 0} \right)\left( {x - \frac{{\sqrt {39} }}{{10}}} \right) + \left( {2 - \frac{3}{2}} \right)\left( {y - 2} \right) = 0\\ \Leftrightarrow \frac{{\sqrt {39} }}{{10}}\left( {x - \frac{{\sqrt {39} }}{{10}}} \right) + \frac{1}{2}\left( {y - 2} \right) = 0\\ \Leftrightarrow \sqrt {39} x + 5y - 13,9 = 0\end{array}\)
30 tháng 9 2023
Sau khi được ném đi, quỹ đạo chuyển động của chiếc đĩa nằm trên tiếp tuyến của đường tròn tâm I tại điểm M.
Vậy quỹ đạo chuyển động của chiếc đĩa nằm trên đường thẳng có phương trình là:
\(\left(\dfrac{\sqrt{39}}{10}-0\right)\left(x-\dfrac{\sqrt{39}}{10}\right)+\left(2-\dfrac{3}{2}\right)\left(y-2\right)=0\\ \Leftrightarrow\dfrac{\sqrt{39}}{10}\left(x-\dfrac{\sqrt{39}}{10}\right)+\dfrac{1}{2}\left(y-2\right)=0\\ \Leftrightarrow\sqrt{39}x+5y-13,9=0\)
HQ
Hà Quang Minh
Giáo viên
24 tháng 9 2023
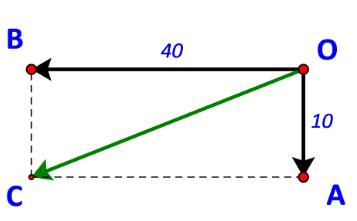
Gọi O là vị trí của ca nô.
Vẽ \(\overrightarrow {OA} \) là vận tốc dòng nước (chảy từ phía bắc xuống phía nam),
\(\overrightarrow {OB} \) là vận tốc riêng của ca nô (chuyển động từ phía đông sang phía tây)
Khi đó vecto vận tốc của ca nô so với bờ sông là vecto \(\overrightarrow {OA} + \overrightarrow {OB} \)
Gọi C là đỉnh thứ tư của hình bình hành OACB, ta có: \(\overrightarrow {OC} = \overrightarrow {OA} + \overrightarrow {OB} \)
Xét tam giác OBC vuông tại B ta có:
BC = 40; BC = OA = 10.
\( \Rightarrow OC = \sqrt {O{B^2} + B{C^2}} = 10\sqrt {17} \)
Vậy vận tốc của ca nô so với bờ sông là \(10\sqrt {17} \) km/h.
24 tháng 9 2023
Tham khảo:
a) Ta có sơ đồ đường đi như sau:
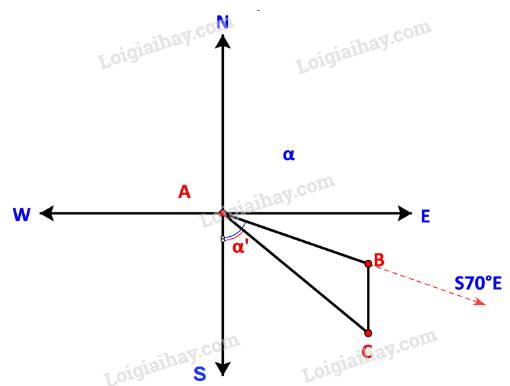
Trong đó: B là nơi động cơ bị hỏng, C là ví trí neo đậu của tàu trên hòn đảo.
Khoảng cách từ cảng A tới đảo nơi tàu neo đậu là đoạn AC.
Quãng đường tàu đi được sau 90 phút hay 1,5 giờ (ngay trước khi hỏng động cơ) là:
70.1,5 = 105 (km) hay AB = 105.
Sau 2 giờ tàu trôi tự do từ B đến C với vận tốc 8km/h , suy ra BC= 8.2 = 16 (km).
Ban đầu tàu di chuyển theo hướng \(S{70^o}E\) nên \(\widehat {BAS} = {70^o}\). Sau khi động cơ bị hỏng, tàu trôi theo hướng Nam do đó BC song song với AS.
\( \Rightarrow \widehat {ABC} = {180^o} - \widehat {BAS} = {110^o}\)
Áp dụng định lí cosin cho tam giác ABC ta có:
\({AC^2} = {BC^2} + {AB^2} - 2.AC.BC.\cos B\)
\(\begin{array}{l} \Rightarrow {AC^2} = {16^2} + {105^2} - 2.16.105.\cos {110^o} \approx 12430\\ \Rightarrow AC \approx 111,5.\end{array}\)
Vậy khoảng cách từ cảng A tới đảo nơi tàu neo đậu là khoảng 111,5 km.
b)
Theo sơ đồ, hướng từ cảng A tới đảo nơi tàu neo đậu là \(S{\alpha ^o}E\) với \({\alpha ^o} = \widehat {CAS}\).
Do BC // AS nên \(\widehat {CAS}= \widehat {ACB}\)
Áp dụng định lí sin cho tam giác ABC ta có:
\(\frac{BC}{{\sin A}} = \frac{AC}{{\sin B}} = \frac{AB}{{\sin C}}\)\( \Rightarrow \sin C = \frac{{AB.\sin B}}{AC}\)
Mà \(\widehat B = {110^o}\); \(AC \approx 111,5\); AB = 105.
\(\begin{array}{l} \Rightarrow \sin C= \frac{{105.\sin {{110}^o}}}{{111,5}} \approx 0,885\\ \Rightarrow \widehat C \approx {62^o}(do\;\widehat C < {90^o})\end{array}\)
Vậy hướng từ cảng A tới đảo nơi tàu neo đậu là \(S{62^o}E\).
2 tháng 1
a: Gọi hàm số bậc hai cần tìm là (P): \(y=ax^2+bx+c\)
Thay x=0 và y=-7 vào (P), ta được:
\(a\cdot0^2+b\cdot0+c=-7\)
=>c=-7
=>(P): \(y=ax^2+bx-7\)
Thay x=-4 và y=10 vào (P), ta được: \(a\cdot\left(-4\right)^2+b\cdot\left(-4\right)-7=10\)
=>16a-4b=17(1)
Thay x=20 và y=5 vào (P), ta được:
\(a\cdot20^2+b\cdot20-7=5\)
=>400a+20b=12(2)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}16a-4b=17\\400a+20b=12\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}80a-20b=85\\400a+20b=12\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}480a=97\\16a-4b=17\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{97}{480}\\4b=16a-17=-\dfrac{413}{30}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}a=\dfrac{97}{480}\\b=-\dfrac{413}{120}\end{matrix}\right.\)
Vậy: (P): \(y=\dfrac{97}{480}x^2-\dfrac{413}{120}x-7\)
24 tháng 9 2023
Tham khảo:
Lấy các điểm: A, C sao cho:
Vectơ vận tốc dòng nước\(\overrightarrow {{v_n}} = \overrightarrow {OA} \)
Vectơ vận tốc chuyển động \(\overrightarrow {{v_{cano}}} = \overrightarrow {OC} \)
Ta có: \(\overrightarrow {{v_{cano}}} = \overrightarrow {{v_n}} + \overrightarrow v \), với \(\overrightarrow v \) là vectơ vận tốc riêng của cano.
Gọi B là điểm sao cho \(\overrightarrow v = \overrightarrow {OB} \) thì OACB là hình bình hành.
Vì tàu chuyển động theo hướng \(S{15^o}E\) nên vectơ \(\overrightarrow {OC} \) tạo với hướng Nam (tia OS) góc \({15^o}\) và tạo với hướng Đông (tia OE) góc \({90^o} - {15^o} = {75^o}\).
Mà nước trên sông chảy về hướng đông nên vectơ \(\overrightarrow {OA} \) cùng hướng với vectơ \(\overrightarrow {OE} \)
Do đó góc tạo bởi vectơ \(\overrightarrow {OC} \) và vectơ \(\overrightarrow {OA} \) là \({75^o}\)
Xét tam giác OAC ta có:
\(OA = \;|\overrightarrow {{v_n}} |\; = 3\); \(OC = \;|\overrightarrow {{v_{cano}}} |\; = 20\) và \(\widehat {AOC} = {75^o}\)
Áp dụng định lí cosin tại đỉnh O ta được:
\(\begin{array}{l}A{C^2} = O{A^2} + O{C^2} - 2.OA.OC.\cos \widehat {AOC}\\ \Leftrightarrow A{C^2} = {3^2} + {20^2} - 2.3.20.\cos {75^o} \approx 378\\ \Leftrightarrow OB = AC \approx 19,44\end{array}\)
Vậy vận tốc riêng của cano là 19,44 km/h
HQ
Hà Quang Minh
Giáo viên
25 tháng 9 2023
Sắp xếp các cân nặng theo thứ tự không giảm, ta được dãy:
50; 52; 52; 54; 54; 56; 56; 57; 58; 58; 59; 61; 61; 62; 64; 65; 66; 67; 68; 69.
+) Vì cỡ mẫu \(n = 20\), là số chẵn, nên giá trị tứ phân vị thứ hai là \({Q_2} = \frac{1}{2}\left( {58 + 59} \right) = 58,5\)
+) Tứ phân vị thứ nhất là trung vị của mẫu: 50; 52; 52; 54; 54; 56; 56; 57; 58; 58.
Do đó \({Q_1} = \frac{1}{2}(54 + 56) = 55\)
+) Tứ phân vị thứ nhất là trung vị của mẫu: 59; 61; 61; 62; 64; 65; 66; 67; 68; 69.
Do đó \({Q_3} = \frac{1}{2}(64 + 65) = 64,5\)
Vậy 3 ngưỡng cân nặng để phân nhóm là: 55kg; 58,5 kg; 64,5 kg.