
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi số sản phẩm àm 2 ng công nhân được giao là x (x∈N*, sản phẩm)
Thời gian hoàn thành công việc của người thứ nhất là: \(\dfrac{x}{40}\left(h\right)\)
Thời gian hoàn thành công việc của ngươi thứ hai là: \(\dfrac{x}{50}\left(h\right)\)
Vì ng thứ nhất hoàn thành công việc chậm hơn người thứ hai 2 giờ nên ta có PT:
\(\dfrac{x}{40}-\dfrac{x}{50}=2\)
⇔\(50x-40x=4000\)
⇔\(10x=4000\)
⇔\(x=400\)
Vậy số sản phẩm mỗi công nhân được giao là 400 (sản phẩm)

Bài 2:
Xé ΔADH vuông tại H và ΔCBK vuông tại K có
AD=BC
\(\widehat{ADH}=\widehat{CBK}\)
Do đó: ΔADH=ΔCBK
Suy ra: AH=CK
Xét tứ giác AHCK có
AH//CK
AH=CK
Do đó: AHCK là hình bình hành

bn chụp màn hình sao vậy? k bt giống bn k alt+ctrl+a
Bài 5:
a: \(x\left(x-1\right)-x^2+4x=-3\)
\(\Leftrightarrow x^2-x-x^2+4x=-3\)
hay x=-1
b: \(6x^2-\left(2x+5\right)\left(3x-2\right)=7\)
\(\Leftrightarrow6x^2-6x^2+4x-15x+10=7\)
\(\Leftrightarrow-11x=-3\)
hay \(x=\dfrac{3}{11}\)

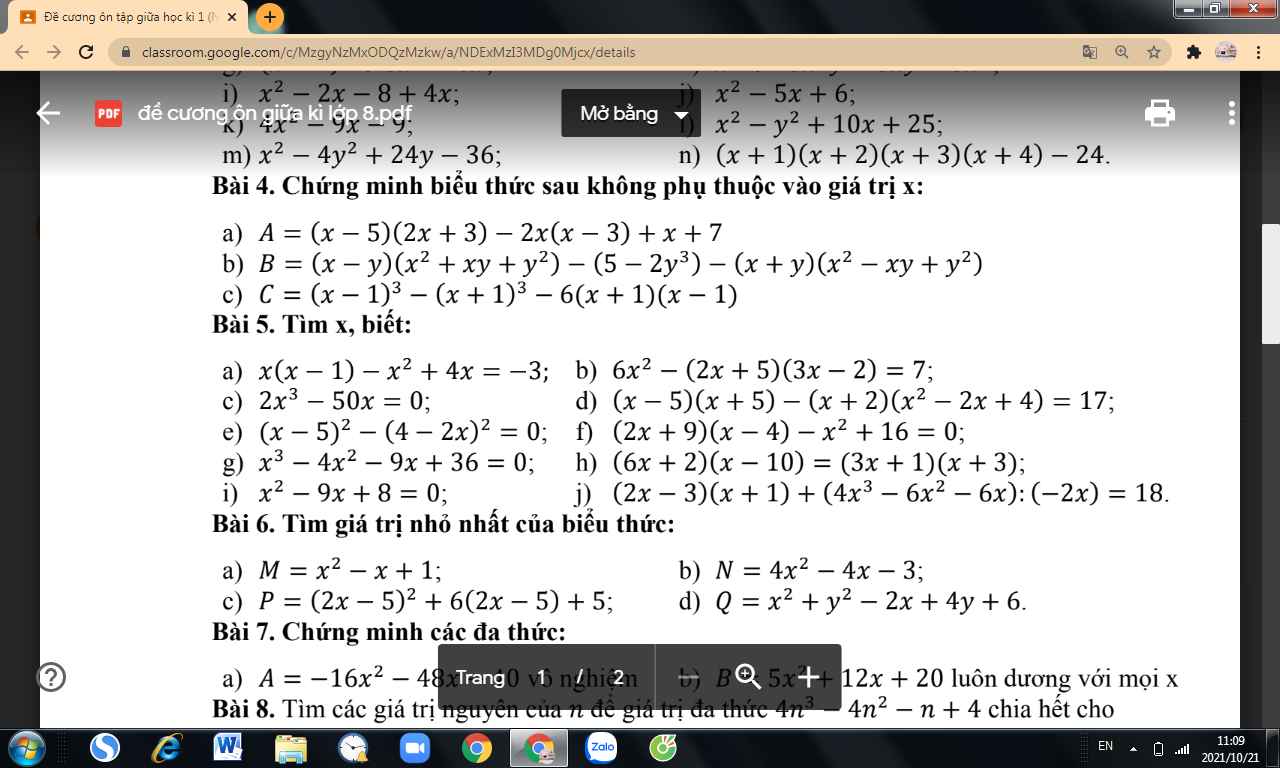
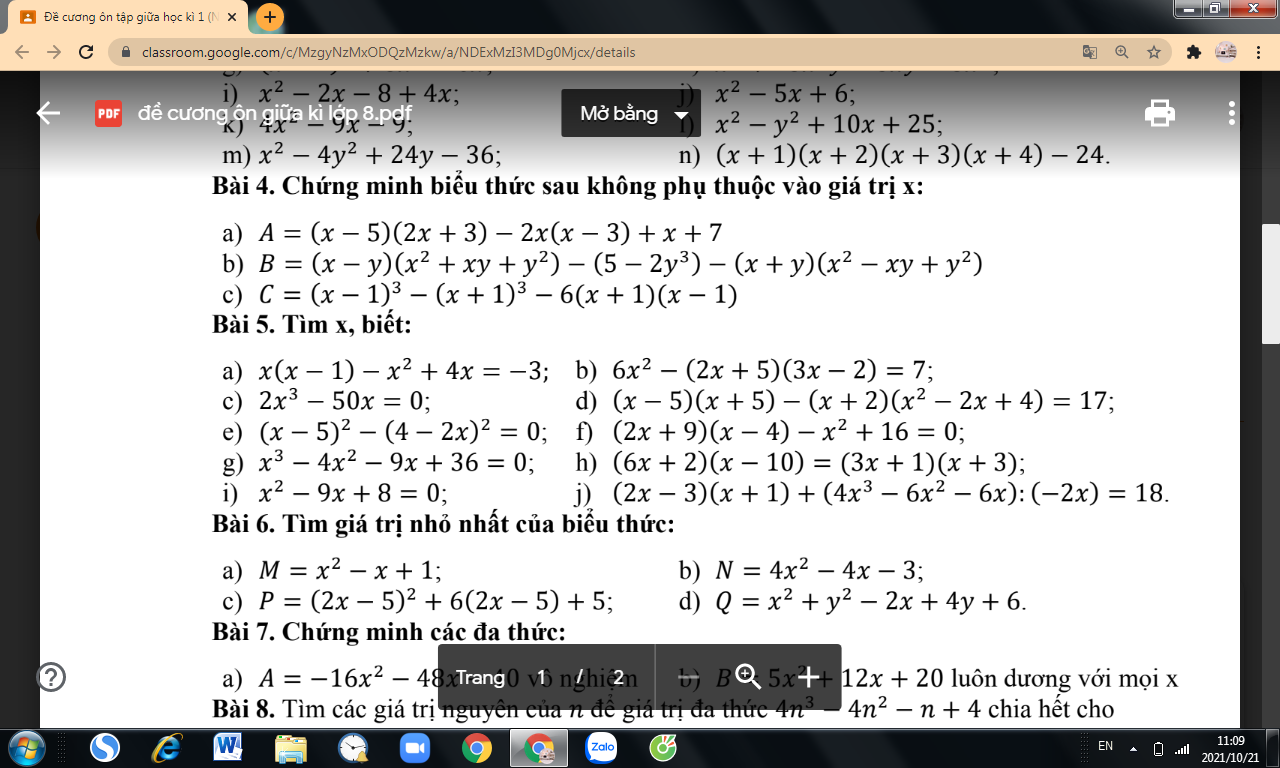
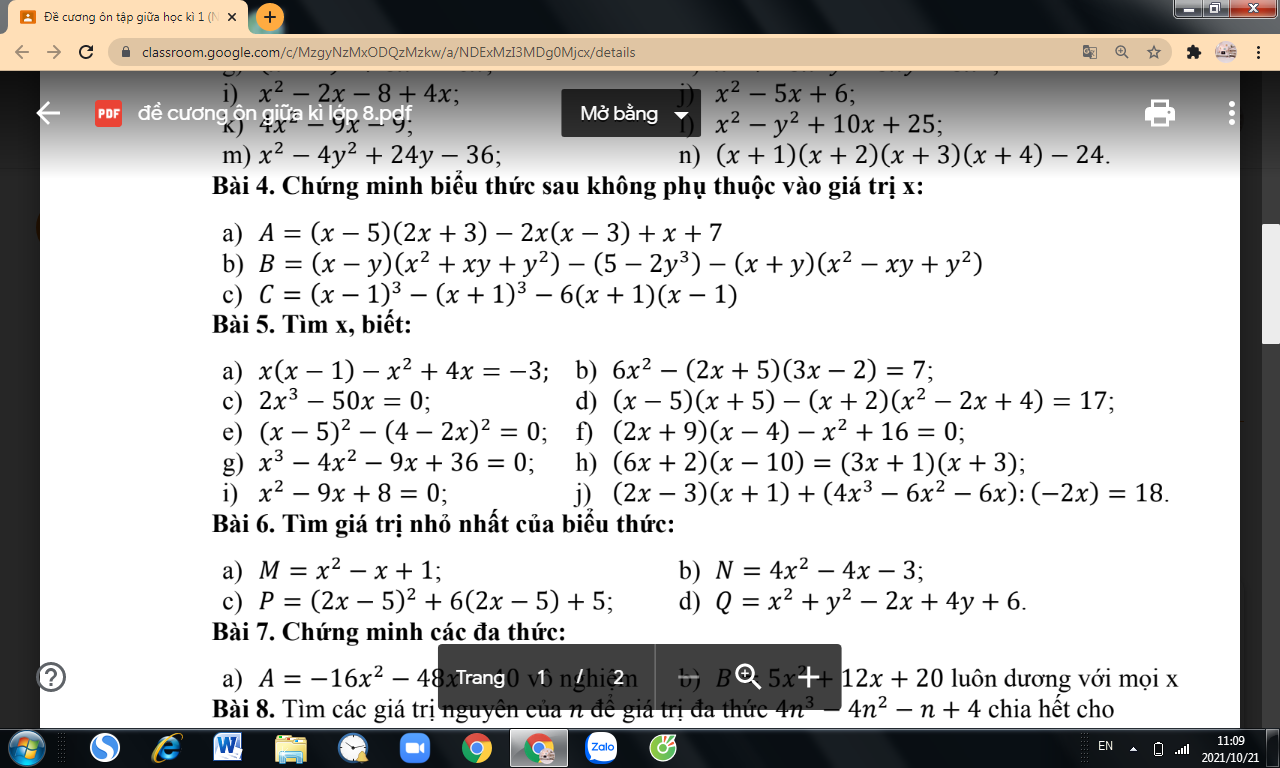
Bài 4:
\(A=2x^2+3x-10x-15-2x^2+6x+x+7=-8\\ B=x^3-y^3-5+2y^3-x^3-y^3=-5\\ C=x^3-3x^2+3x-1-x^3-3x^2-3x-1-6x^2+6=4\)

Bài 5:
a: \(x\left(x-1\right)-x^2+4x=-3\)
\(\Leftrightarrow x^2-x-x^2+4x=-3\)
hay x=-1
i: \(x^2-9x+8=0\)
\(\Leftrightarrow\left(x-1\right)\left(x-8\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=8\end{matrix}\right.\)

Bài 1:
a: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình của ΔABC
Suy ra: MN//BC và \(MN=\dfrac{BC}{2}\)
hay MN//BP và MN=BP
Xét tứ giác BMNP có
MN//BP
MN=BP
Do đó: BMNP là hình bình hành


Bài 4:
b: \(B=\left(x-y\right)\left(x^2+xy+y^2\right)+2y^3-5-\left(x+y\right)\left(x^2-xy+y^2\right)\)
\(=x^3-y^3+2y^3-5-x^3-y^3\)
=-5
c: \(C=\left(x-1\right)^3-\left(x+1\right)^3-6\left(x+1\right)\left(x-1\right)\)
\(=x^3-3x^2+3x-1-x^3-3x^2-3x-1-6\left(x^2-1\right)\)
\(=-6x^2-2-6x^2+6\)
\(=-12x^2+4\)

Bài 6:
\(\dfrac{x-1}{2013}+\dfrac{x-2}{2012}+\dfrac{x-3}{2011}=\dfrac{x-4}{2010}+\dfrac{x-5}{2009}+\dfrac{x-6}{2008}\)
⇔\(\dfrac{x-1}{2013}-1+\dfrac{x-2}{2012}-1+\dfrac{x-3}{2011}-1=\dfrac{x-4}{2010}-1+\dfrac{x-5}{2009}-1+\dfrac{x-6}{2008}-1\)⇔\(\dfrac{x-2014}{2013}+\dfrac{x-2014}{2012}+\dfrac{x-2014}{2011}=\dfrac{x-2014}{2010}+\dfrac{x-2014}{2009}+\dfrac{x-2014}{2008}\)
⇔\(\dfrac{x-2014}{2013}+\dfrac{x-2014}{2012}+\dfrac{x-2014}{2011}-\dfrac{x-2014}{2010}-\dfrac{x-2014}{2009}-\dfrac{x-2014}{2008}=0\)
⇔\(\left(x-2014\right)\left(\dfrac{1}{2013}+\dfrac{1}{2012}+\dfrac{1}{2011}-\dfrac{1}{2010}-\dfrac{1}{2009}-\dfrac{1}{2008}\right)=0\)
Vì \(\dfrac{1}{2013}+\dfrac{1}{2012}+\dfrac{1}{2011}-\dfrac{1}{2010}-\dfrac{1}{2009}-\dfrac{1}{2008}\ne0\)
\(\Rightarrow x-2014=0\)
⇔\(x=2014\).
-Vậy \(S=\left\{2014\right\}\).
Bài 7:
\(x^2-4x+y^2-6y+15=2\)
⇔\(x^2-4x+y^2-6y+15-2=0\)
⇔\(x^2-4x+y^2-6y+13=0\)
⇔\(\left(x^2-4x+4\right)+\left(y^2-6y+9\right)=0\)
⇔\(\left(x-2\right)^2+\left(y-3\right)^2=0\)
Vì \(\left(x-2\right)^2\ge0,\left(y-3\right)^2\ge0\).
\(\Rightarrow\)\(\left(x-2\right)^2=0\) và \(\left(y-3\right)^2=0\)
⇔\(x=2\) và \(y=3\).
Bài 8:
\(\left(x^2+1\right)^2+3x\left(x^2+1\right)+2x^2=0\)
⇔\(\left(x^2+1\right)^2+2x\left(x^2+1\right)+x^2+x\left(x^2+1\right)+x^2=0\)
⇔\(\left(x^2+1+x\right)^2+x\left(x^2+1+x\right)=0\)
⇔\(\left(x^2+1+x\right)\left(x^2+1+x+x\right)=0\)
⇔\(x^2+x+1=0\) (vô nghiệm, bạn tự c/m) hay \(x^2+2x+1=0\)
⇔\(x^2+2x+1=0\)
⇔\(\left(x+1\right)^2=0\)
⇔\(x=-1\).
-Vậy \(S=\left\{-1\right\}\)

 em cần giải gấp bài 3 chi tiết mọi người giúp em với ạ. Làm bài dưới dạng phân số ạ em cần gấp
em cần giải gấp bài 3 chi tiết mọi người giúp em với ạ. Làm bài dưới dạng phân số ạ em cần gấp







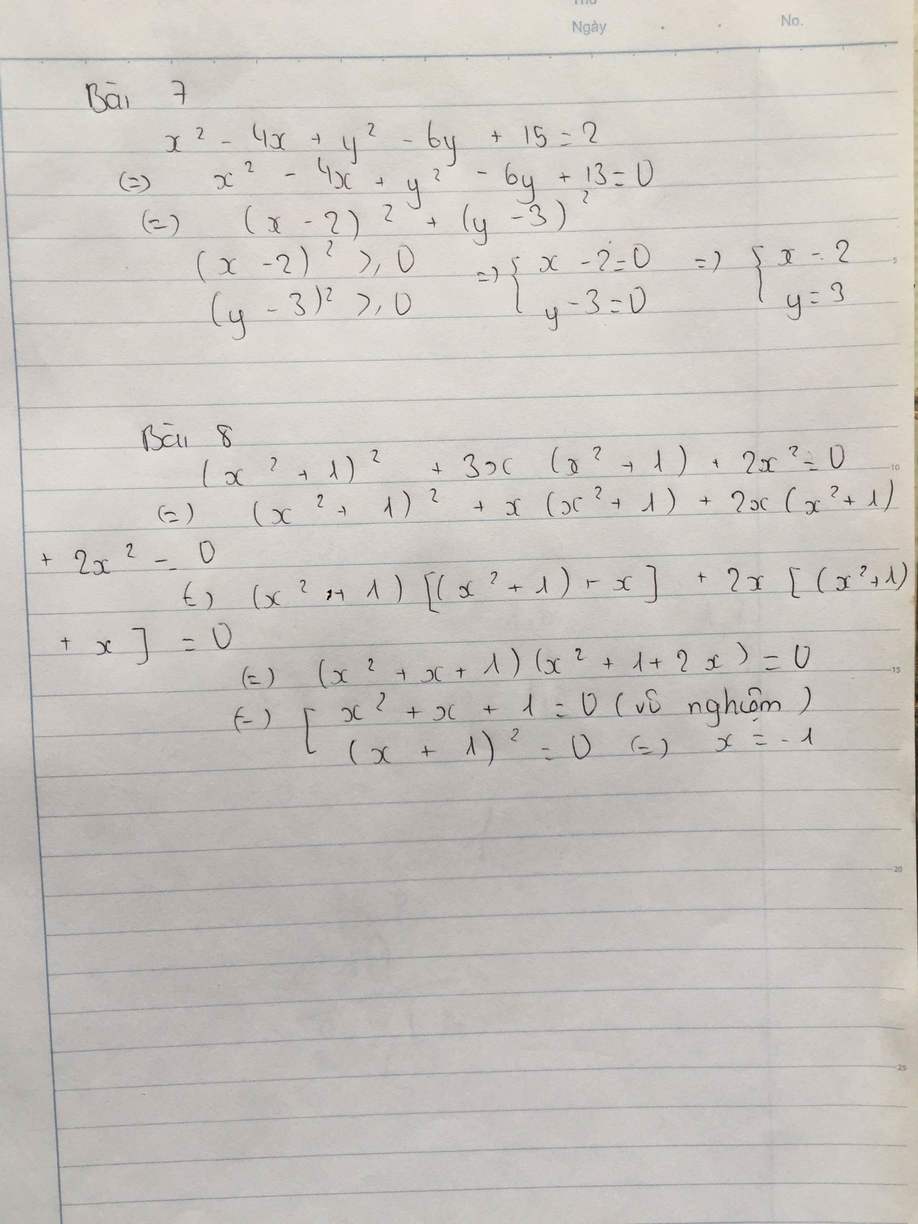
Giúp em với ạ huhu