
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a:
ΔMAB vuông tại M
=>ΔMAB nội tiếp đường tròn đường kính AB
mà ΔMAB nội tiếp (O)
nên AB là đường kính của (O)
Xét (O) có
ΔAEB nội tiếp
AB là đường kính
Do đó: ΔAEB vuông tại E
=>BE\(\perp\)EA tại E
=>BE\(\perp\)AF tại E
Xét ΔBAF có
BE là đường cao
BE là đường phân giác
Do đó:ΔBAF cân tại B
b: Xét ΔBAH và ΔBFH có
BA=BF
\(\widehat{ABH}=\widehat{FBH}\)
BH chung
Do đó: ΔBAH=ΔBFH
=>\(\widehat{BAH}=\widehat{BFH}\)
=>\(\widehat{BFH}=90^0\)
=>HF là tiếp tuyến của (B;BA)
c: Xét ΔFAB có
AM,BH là đường cao
AM cắt BH tại K
Do đó: K là trực tâm của ΔFAB
=>FK\(\perp\)AB tại P
Xét tứ giác KMBP có \(\widehat{KMB}+\widehat{KPB}=90^0+90^0=180^0\)
nên KMBP là tứ giác nội tiếp
=>K,M,B,P cùng thuộc một đường tròn

a) \(D=4\sqrt{\dfrac{1}{3}}+5\sqrt{12}-6\sqrt{27}\)
\(=\dfrac{4}{9}\sqrt{3}+5.2\sqrt{3}-6.3\sqrt{3}\)
\(=\dfrac{4}{9}\sqrt{3}+10\sqrt{3}-18\sqrt{3}\)
\(=-\dfrac{68}{9}\sqrt{3}\)
b) \(E=\dfrac{2}{\sqrt{3}-1}-\sqrt{4-2\sqrt{3}}\)
\(=\dfrac{2\left(\sqrt{3}+1\right)}{2}-\sqrt{\left(\sqrt{3}\right)^2-2.\sqrt{3}.1+1^2}\)
\(=\sqrt{3}+1-\sqrt{\left(\sqrt{3}-1\right)^2}\)
\(=\sqrt{3}+1-\left(\sqrt{3}-1\right)\)
\(=\sqrt{3}+1-\sqrt{3}+1=2\)
c) \(F=\dfrac{\sqrt{15}-\sqrt{10}}{\sqrt{3}-\sqrt{2}}+\dfrac{3}{2-\sqrt{5}}\)
\(=\dfrac{\sqrt{5}\left(\sqrt{3}-\sqrt{2}\right)}{\sqrt{3}-\sqrt{2}}+\dfrac{3\left(2+\sqrt{5}\right)}{-1}\)
\(=\sqrt{5}-6-3\sqrt{5}=-2\sqrt{5}-6\)


\(g,ĐK:x\ge0\\ PT\Leftrightarrow10\sqrt{x}+8\sqrt{x}-11\sqrt{x}=21\\ \Leftrightarrow\sqrt{x}=3\Leftrightarrow x=9\left(tm\right)\\ h,ĐK:x\ge0\\ PT\Leftrightarrow6\sqrt{3x}+2\sqrt{3x}-3\sqrt{3x}=15\\ \Leftrightarrow\sqrt{3x}=5\Leftrightarrow3x=25\Leftrightarrow x=\dfrac{25}{3}\left(tm\right)\\ i,ĐK:x\ge0\\ PT\Leftrightarrow12\sqrt{x}-21-2\sqrt{x}+10=6\sqrt{x}-12\\ \Leftrightarrow4\sqrt{x}=-1\Leftrightarrow\sqrt{x}=-\dfrac{1}{4}\Leftrightarrow x\in\varnothing\\ j,ĐK:x\ge2\\ PT\Leftrightarrow6\sqrt{x-2}-15\cdot\dfrac{1}{5}\sqrt{x-2}=20+4\sqrt{x-2}\\ \Leftrightarrow\sqrt{x-2}=-20\Leftrightarrow x\in\varnothing\)
\(k,ĐK:x\ge3\\ PT\Leftrightarrow6\sqrt{x-3}-\dfrac{1}{5}\cdot5\sqrt{x-3}-\dfrac{1}{7}\cdot7\sqrt{x-3}=20\\ \Leftrightarrow4\sqrt{x-3}=20\Leftrightarrow\sqrt{x-3}=5\\ \Leftrightarrow x-3=25\Leftrightarrow x=28\left(tm\right)\\ l,ĐK:x\ge5\\ PT\Leftrightarrow2\sqrt{x-5}+\sqrt{x-5}-\dfrac{1}{3}\cdot3\sqrt{x-5}=4\\ \Leftrightarrow2\sqrt{x-5}=4\Leftrightarrow\sqrt{x-5}=2\\ \Leftrightarrow x-5=4\Leftrightarrow x=9\left(tm\right)\)

A
ĐKXĐ: \(\left\{{}\begin{matrix}-x\ge0\\x^2-1\ne0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x\le0\\x\ne\pm1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x\le0\\x\ne-1\end{matrix}\right.\)

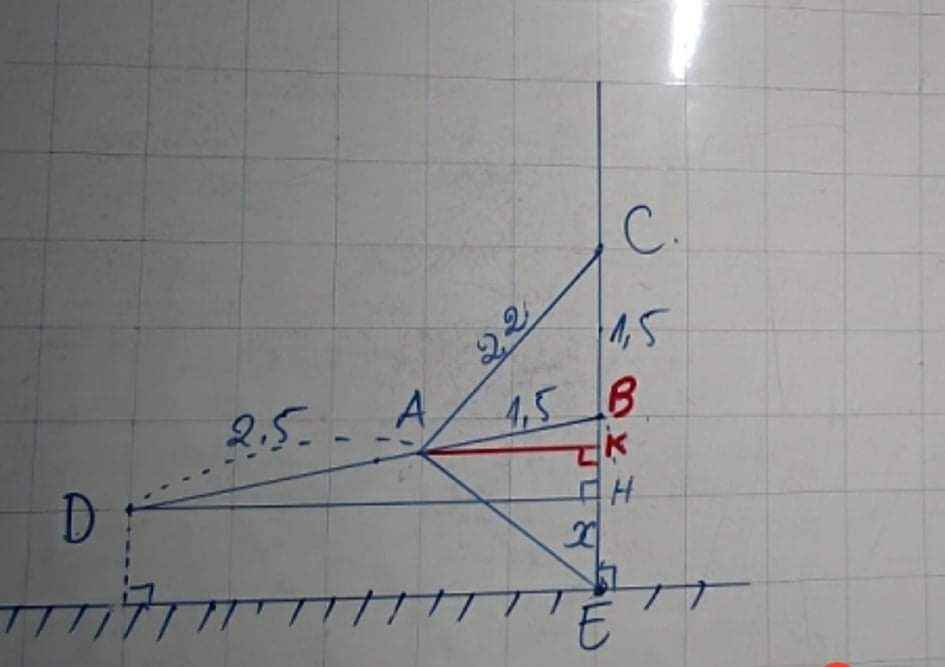
Gọi DH là khoảng cách thấp nhất từ máy bay đến mặt đất, khi đó AC có độ dài lớn nhất là 2,2m. Dựng hình chữ nhật DHEK => DH = EK
Do BA = BE = BC = 1,5m cố định nên tam giác ACE vuông tại A
Xét tam giác ACE vuông tại A có cos\(\widehat{ECA}\) = \(\dfrac{CA}{CE}=\dfrac{2,2}{3}\) => \(\widehat{ECA}\) \(\approx\) 42o50'
BA = BC => tam giác ABC cân tại B => \(\widehat{BAC}=\widehat{BCA}\) = \(\widehat{ECA}\) \(\approx\) 42o50'
=> \(\widehat{DBK}\) = \(\widehat{BAC}+\widehat{BCA}\) = 2.\(\widehat{BCA}\) = 85o40'
Xét tam giác DBK vuông tại D có: BK = BD. cos\(\widehat{DBK}\)
= 4.cos85o40' \(\approx\) 0,3022
=> DH = KE \(\approx\) 1,5 - 0,3022 \(\approx\)1,2 (m)

x + 3y = x(5y - 1) (1)
1/x - 3/y = -2 (2)
(1) ⇔ x(5y - 1) - x = 3y
⇔ x(5y - 2) = 3y
⇔ x = 3y/(5y - 2) (3)
Thế (3) vào (2) ta được:
(2) ⇔ 1/[3y/(5y - 2)] - 3/y = -2
⇔ (5y - 2)/3y - 3/y = -2
⇔ 5y - 2 - 9 = -6y
⇔ 5y + 6y = 11
⇔ 11y = 11
⇔ y = 1 thế vào (3) ta được:
x = 3.1/(5.1 - 2) = 1
Vậy S = {(1; 1)}

a: Ta có: BC⊥BA tại B
nên BC là tiếp tuyến của (A;AB)
b: Xét (A) có
CB là tiếp tuyến
CD là tiếp tuyến
Do đó: CB=CD
hay C nằm trên đường trung trực của BD(1)
Ta có: AB=AD
nên A nằm trên đường trung trực của BD(2)
Từ (1) và (2) suy ra AC là đường trung trực của BD
hay AC\(\perp\)BD
Giúp mình luôn câu c d được không:((( sắp hết h rồi mà không bt làm
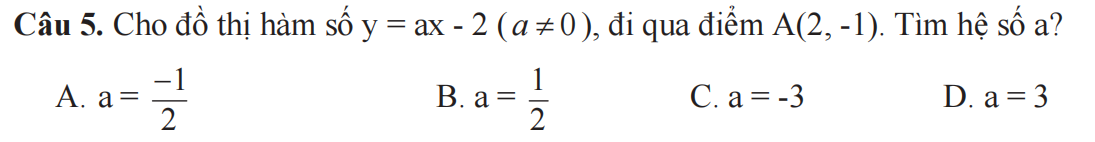


 giúp em với cần gấp ạ huhu
giúp em với cần gấp ạ huhu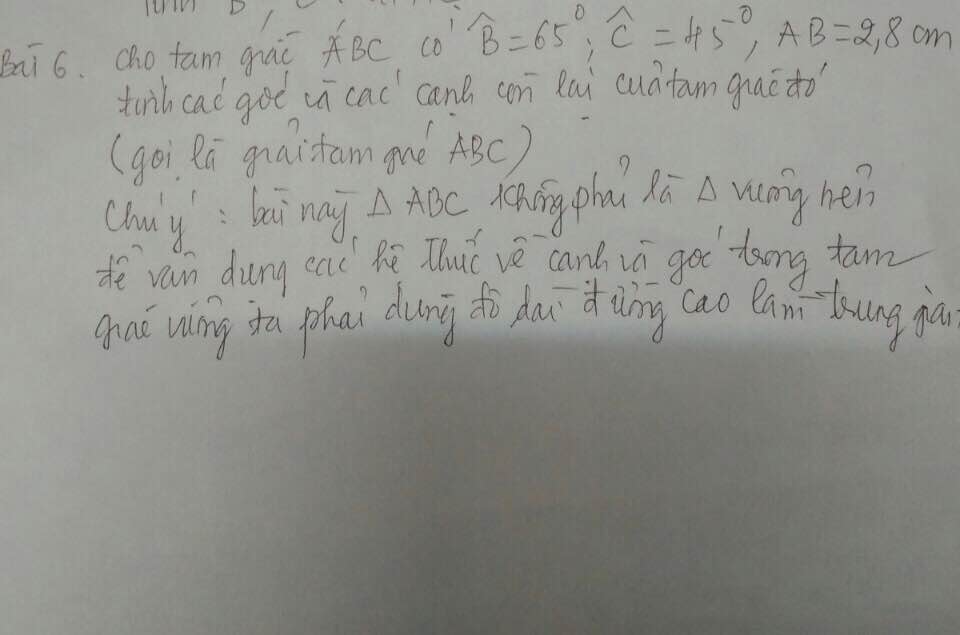
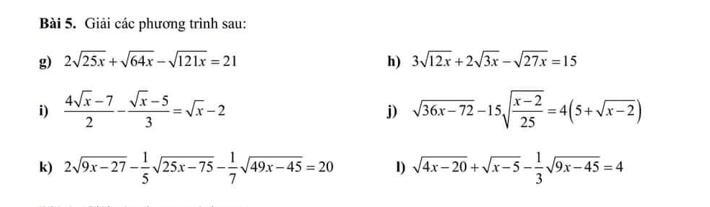




câu B
cho mình lời giải với đc ko bạn :((