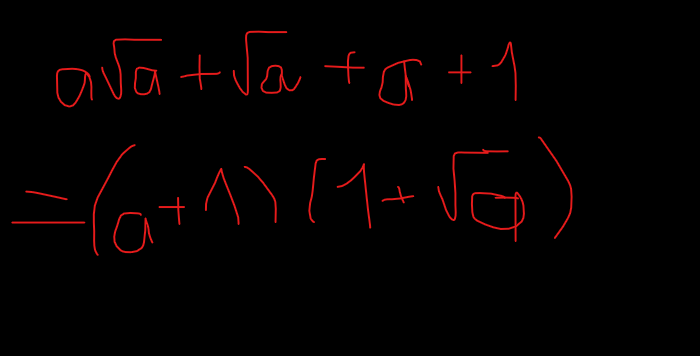K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TT
0
MT
1
NV
Nguyễn Việt Lâm
Giáo viên
15 tháng 10 2019
\(\Leftrightarrow x^3+x^2+x+1=4y^2+4y+1\)
\(\Leftrightarrow\left(x^2+1\right)\left(x+1\right)=\left(2y+1\right)^2\)
Do vế phải lẻ \(\Rightarrow x^2+1\) và \(x+1\) đều lẻ
Gọi \(d=ƯC\left(x^2+1;x+1\right)\Rightarrow d\) lẻ
\(\Rightarrow x\left(x+1\right)-\left(x^2+1\right)⋮d\Rightarrow x-1⋮d\)
\(\Rightarrow\left(x+1\right)-\left(x-1\right)⋮d\Rightarrow2⋮d\Rightarrow d=1\)
\(\Rightarrow x^2+1\) và \(x+1\) nguyên tố cùng nhau
\(\Rightarrow\left\{{}\begin{matrix}x^2+1=a^2\\x+1=b^2\end{matrix}\right.\) với \(a;b\) nguyên tố cùng nhau
\(\Rightarrow\) \(x^2+1\) là số chính phương \(\Rightarrow x^2\) và \(x^2+1\) là 2 số chính phương liên tiếp
Mà số chính phương liên tiếp với \(x^2\) là \(\left(x+1\right)^2\)
\(\Rightarrow x^2+1=\left(x+1\right)^2\Rightarrow2x=0\Rightarrow x=0\)
\(\Rightarrow\left(2y+1\right)^2=1\Rightarrow\left[{}\begin{matrix}y=0\\y=-1\end{matrix}\right.\)
PA
1
12 tháng 4 2022
\(a\sqrt{a}+\sqrt{a}+a+1\)
\(=\sqrt{a}\left(a+1\right)+\left(a+1\right)\)
\(=\left(a+1\right)\left(\sqrt{a}+1\right)=\left(a+1\right)\left(1+\sqrt{a}\right)\)
Đặt \(\sqrt{a}\) ra đó bạn
AN
1
2
22 tháng 5 2023
Ptr có `2` nghiệm phân biệt `<=>\Delta' > 0`
`=>(m+1)^2-m^2+2m-3 > 0`
`<=>m^2+2m+1-m^2+2m-3 > 0`
`<=>m > 1/2`
`=>` Áp dụng Viét có: `{(x_1+x_2=-b/a=2m+2),(x_1.x_2=c/a=m^2-2m+3):}`
Ta có: `1/[x_1 ^2]-[4x_2]/[x_1]+3x_2 ^2=0`
`=>1-4x_1.x_2+3(x_1.x_2)^2=0`
`<=>1-4(m^2-2m+3)+3(m^2-2m+3)^2=0`
`<=>[(m^2-2m+3=1),(m^2-2m+3=1/3):}`
`<=>[(m^2-2m+2=0(VN)),(m^2-2m+8/3=0(VN)):}`
`=>` Không có `m` thỏa mãn.
MC
18 tháng 10 2018
a, \(\sqrt{8}+\sqrt{18}-\sqrt{\frac{1}{2}}=2\sqrt{2}+3\sqrt{2}-\frac{1}{2}\sqrt{2}\)
\(=\frac{9}{2}\sqrt{2}\)
b, \(\frac{3-\sqrt{3}}{\sqrt{3}}+\frac{2\sqrt{2}}{\sqrt{2}+1}-\left(\sqrt{2}+\sqrt{3}\right)\)
\(=\frac{\sqrt{3}\left(\sqrt{3}-1\right)}{\sqrt{3}}+\frac{2\sqrt{2}}{\sqrt{2}+1}-\sqrt{2}-\sqrt{3}\)
\(=\sqrt{3}-1+\frac{2\sqrt{2}}{\sqrt{2}+1}-\sqrt{2}-\sqrt{3}\)
\(=\frac{2\sqrt{2}}{\sqrt{2}+1}-\left(\sqrt{2}+1\right)\) \(=\frac{2\sqrt{2}-\left(\sqrt{2}+1\right)^2}{\sqrt{2}+1}\)
\(=\frac{2\sqrt{2}-2-2\sqrt{2}-1}{\sqrt{2}+1}=-\frac{2+1}{\sqrt{2}+1}\)
c, PT xác định với mọi x nha!
\(\sqrt{x^2-2x+1}=3\) \(\Rightarrow x^2-2x+1=9\)
\(\Leftrightarrow x^2-2x-8=0\)
\(\Leftrightarrow\left(x^2-4x\right)+\left(2x-8\right)=0\)
\(\Leftrightarrow\left(x-4\right)\left(x+2\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-4=0\\x+2=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=4\\x=-2\end{cases}}}\)
Vậy...
bạn tự kl
22 tháng 7 2018
Nhận xét : Điều kiện để hàm số \(y=ax+b\) đồng biến là \(a>0\).
Với \(a=m^2+m+1;b=-2\)
Ta thấy \(a=\left(m+\frac{1}{2}\right)^2+\frac{3}{4}>0\forall m\) nên hàm số \(y=\left(m^2+m+1\right)x-2\) đồng biến
6 tháng 11 2018
\(\sqrt{4x+1}+\sqrt{3x-2}=5\)
ĐKXĐ :\(\hept{\begin{cases}4x+1\ge0\\3x-2\ge0\end{cases}\Leftrightarrow\hept{\begin{cases}x\ge-\frac{1}{4}\\x\ge\frac{2}{3}\end{cases}\Leftrightarrow x\ge\frac{2}{3}}}\)
Pt \(\Rightarrow\sqrt{4x+1}=5-\sqrt{3x-2}\)
\(\Leftrightarrow4x+1=\left(5-\sqrt{3x-2}\right)^2\)
\(\Leftrightarrow4x+1=25-10\sqrt{3x-2}+3x-2\)
\(\Leftrightarrow10\sqrt{3x-2}=-4x-1+25+3x-2\)
\(\Leftrightarrow10\sqrt{3x-2}=-x+22\)
\(\Leftrightarrow\left(10\sqrt{3x-2}\right)^2=\left(-x+22\right)^2\)
\(\Leftrightarrow100\left(3x-2\right)=484-44x+x^2\)
\(\Leftrightarrow300x-200=484-44x+x^2\)
\(\Leftrightarrow684-344x+x^2=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=342\\x=2\end{cases}}\)Tm
P/s ko bt có sai ở chỗ nào ko , bn tham khảo nha