
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\frac{5x-1}{3}=\frac{7y-6}{5}=\frac{5x-1-7y+6}{3-5}=\frac{5x-7y+5}{-2}=\frac{5x-7y-7}{4x}\)
\(\frac{5x-7y+5}{-2}=\frac{5x-7y-7}{4x}=\frac{5x-7y+5-5x+7y+7}{-2-4x}=\frac{12}{-2-4x}\)
\(\Rightarrow\frac{5x-1}{3}=\frac{6}{-1-2x}\)
Giải ra tìm x thế vào PT đầu tiên để tìm y



Từ \(\frac{5x-1}{3}=\frac{7y-6}{5}\) Áp dụng TC DTSBN ta có :
\(\frac{5x-1}{3}=\frac{7y-6}{5}=\frac{\left(5x-1\right)+\left(7y-6\right)}{3+5}=\frac{5x+7y-7}{8}=\frac{5x+7y-7}{4x}\)
\(\Rightarrow4x=8\Rightarrow x=2\)
\(\Rightarrow\frac{5.2-1}{3}=\frac{7y-6}{5}\)
\(\Leftrightarrow\frac{7y-6}{5}=3\)
\(\Rightarrow y=3\)
Vậy \(x=2;y=3\)
\(\frac{5x-1}{3}=\frac{7y-6}{5}\Rightarrow5\left(5x-1\right)=3\left(7y-6\right)\Rightarrow25x-5=21y-18\)
\(\Rightarrow21y=25x+13\Rightarrow7y=\frac{25x+13}{3}\)
Xét : \(\frac{5x+7y-7}{4x}=\frac{5x+\frac{25x+13}{3}-7}{4x}=\frac{10x-2}{3x}\)
\(\Rightarrow3x\left(5x-1\right)=3\left(10x-2\right)\Rightarrow15x^2-33x+6=0\)
\(\Rightarrow3\left(x-2\right)\left(5x-1\right)=0\Rightarrow\orbr{\begin{cases}x=2\\x=\frac{1}{5}\end{cases}}\)
Với x=2 , ta có : y=3
Với x =\(\frac{1}{5}\), ta có : y= \(\frac{6}{7}\)


(x - 7)x+1 - (x - 7)x+1 = 0
<=> 0 = 0
Vậy phương trình có nghiệm với mọi x thuộc R
b/ Chi cần áp dụng tính chất dãy tỷ số bằng nhau thì ra thôi

\(.a.\)
\(\left(x-7\right)^{x+1}-\left(x-7\right)^{x+1}=0\)
\(\Leftrightarrow\left(x-7\right)^{x+1}.\left[1-\left(x-7\right)^{10}\right]=0\)
\(\Leftrightarrow\left[\begin{matrix}\left(x-7\right)^{x+1}=0\\\left[1-\left(x-7\right)^{10}\right]=0\end{matrix}\right.\)
+ Nếu \(\left(x-7\right)^{x+1}=0\)
\(\Rightarrow x-7=0\)
\(\Rightarrow x=0+7\)
\(\Rightarrow x=7\)
+ Nếu \(1-\left(x-7\right)^{10}=0\)
\(\Rightarrow\left(x-7\right)^{10}=1\)
\(\Rightarrow\left(x-7\right)^{10}=\left(\pm1\right)^{10}\)
\(\Rightarrow\left[\begin{matrix}x-7=1\\x-7=-1\end{matrix}\right.\)
\(\Rightarrow\left[\begin{matrix}x=1+7\\x=-1+7\end{matrix}\right.\)
\(\Rightarrow\left[\begin{matrix}x=8\\x=6\end{matrix}\right.\)
Vậy : \(x\in\left\{6;7;8\right\}\)

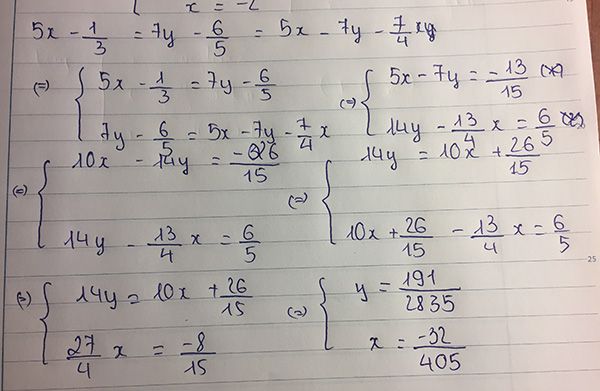
cộng 2 đầu ra x=2 nên y=3
bài này dễ quá