
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đáp án A
Đặt x = - t ⇒ L = lim x → + ∞ t 2 + t - 2 t 3 - 4 t = lim x → + ∞ 1 + 1 t - 2 3 t - 4 = 1 - 2 - 4 = 1 4

a)35cm= 0,35 m = 7/20 m
1,2 dm= 0,12 m = 3/25 m
b) ta có: 7/12 = 7/12.60=35 phút
vì 35 phút < 37 phút nên 7/12 < 37 phút

a.
35cm = 0,35 m
1,2 dm =0,12 m
b. vì \(\frac{7}{12}\)= 35 phút mà 35 phút < 37 phút nên \(\frac{7}{12}\) < 37 phút

Đáp án B
Ta có A = a 5 3 . a 7 3 a 4 . a − 2 7 = a 5 3 . a 7 3 a 4 . a − 2 7 = a 5 3 + 7 3 a 4 − 2 7 = a 2 7
Suy ra m = 2 , n = 7. Do đó 2 m 2 + n = 15
Ghi chú: với m = 2 , n = 7. thì m 2 + n 2 = 53 , m 2 − n 2 = − 45 , 3 m 2 − 2 n = − 2

Đáp án D
Ta có: A = a 5 3 . a 7 3 a 4 . a − 2 7 = a 5 3 × a 7 3 a 4 × a − 2 7 = a 5 3 + 7 3 a 4 − 2 7 = a 4 a 26 7 = a 2 7 = a m n ⇒ m = 2 n = 7 . Vậy 2 m 2 + n = 15

gọi a là UCLN của tử và mẫu
suy ra 2n+1 chia hết cho a suy ra 6n+3 chia hết cho a
ta có 3n+2 chia hết cho a suy ra 6n +4 chia hết cho a
từ hai điều trên suy ra
(6n+4)-(6n+3) chia hết cho a
suy ra 1 chia hết cho a
suy ra a=1
suy ra đpcm
Gọi ƯCLN (2n+1,3n+2)=d
\(\Rightarrow2n+1⋮d\)
\(3n+2⋮d\)
\(\Rightarrow3n+2-2n+1⋮d\)
\(2\left(3n+2\right)-3\left(2n+1\right)⋮d\)
\(6n+4-6n+3⋮d\)
\(\Rightarrow1⋮d\Leftrightarrow d=1\)
Vậy ƯCLN \(\left(2n+1,3n+2\right)=1\Leftrightarrow\dfrac{2n+1}{3n+2}\) là p/s tối giản \(\left(dpcm\right)\)
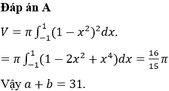
15/17
\(\frac{15}{17}\)