
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


- Xét △OBC có: \(BC\)//\(AD\) (gt).
=>\(\dfrac{OD}{OC}=\dfrac{OA}{OB}\) (định lí Ta-let).
=>\(OD=\dfrac{OA}{OB}.OC=\dfrac{2,5}{2}.3=3,75\) (cm).

Tớ ko giúp đc)): cọu tự tra google đuy,chứ có google để làm j ((:?

Lời giải:
$4x-6=2x+4$
$\Leftrightarrow (4x-6)-(2x+4)=0$
$\Leftrightarrow 2x-10=0$
$\Leftrightarrow 2x=10$
$\Leftrightarrow x=5$

a) Vì AB // CD ⇒ \(\widehat{ABD}=\widehat{ODC}\) ( 2 góc so le trong )
Hay \(\widehat{ABO}=\widehat{ODC}\)
Xét △ AOB và △ COD có:
\(\widehat{ABO}=\widehat{CDO}\) ( chứng minh trên )
\(\widehat{AOB}=\widehat{COD}\) ( đối đỉnh )
⇒ △ AOB ∼ △ COD ( g - g )
b) Vì △ AOB ∼ △ COD
⇒ \(\dfrac{OA}{OC}=\dfrac{AB}{CD}\Rightarrow\dfrac{OA}{6}=\dfrac{5}{10}\)
\(\Rightarrow OA=3cm\)
Vì OE // DC nên theo định lí Ta - lét ta có:
\(\dfrac{OE}{BC}=\dfrac{OA}{AC}\Rightarrow\dfrac{OE}{10}=\dfrac{3}{3+6}\)
\(\Rightarrow OE\approx3,3cm\)

A. TRẮC NGHIỆM: (2,5 điểm) Học sinh chọn câu trả lời đúng cho mỗi câu hỏi sau rồi ghi vào giấy làm bài.
Câu 1 . Biểu thức còn thiếu của hằng đẳng thức: là:
A. 4 xy
B. - 4xy
C. 2 xy
D. -2 x y
Câu 2. Kết quả của phép nhân: bằng:
A.
B.
C.
D.
Câu 3. Kết quả của rút gọn biểu thức :
A. x2 + 4x - 2
B. x2 - 4x + 4
C. x2 + 4x + 4
D. x2 - 4x - 4
Câu 4 . Phân thức nghịch đảo của phân thức là phân thức nào sau đây :
A.
B.
C.
D.
Câu 5 . Phân thức đối của phân thức là :
A.
B.
C.
D. Cả A, B, C đều đúng
Câu 6 . Hình nào sau đây có 4 trục đối xứng ?
A. Hình thang cân
B. Hình bình hành
C. Hình chữ nhật
D. Hình vuông
Câu 7 . Cho hình thang ABCD có AB/ / CD, thì hai cạnh đáy của nó là :
A. AB ; CD
B. AC ;BD
C. AD; BC
D. Cả A, B, C đúng
Câu 8 . Cho hình bình hành ABCD có số đo góc , vậy số đo góc D bằng:
A. 700
B. 750
C. 800
0.850
Câu 9. Một miếng đất hình chữ nhật có độ dài 2 cạnh lần lượt là 4m và 6m ; người ta làm bồn hoa hình vuông cạnh 2m, phần đất còn lại để trồng cỏ, hỏi diện tích trồng cỏ là bao nhiêu m2?
A. 24
B. 16
C. 20
D. 4
Câu 10. Số đo một góc trong của ngũ giác đều là bao nhiêu độ ?
A. 1200
B. 1080
C. 720
D. 900
B. TỰ LUẬN (7,5 điểm)
Bài 1 (1,25 điểm) Phân tích các đa thức sau thành nhân tử
a)
b)
Bài 2 (1,25 điểm) Cho 2 đa thức : và B=2 x+1
a) Tìm đa thức thương và dư trong phép chia A cho B
b) Tìm m để A chia hết cho B
Bài 3. (1,5 điểm) Thực hiện rút gọn các biểu thức:
a)
b)
Bài 4. (3,5 điểm) Cho tam giác ABC, gọi D, E, F lần lượt là trung điểm của các cạnh AB, AC, BC; và M, N, P, Q theo thứ tự là trung điểm các đoạn thẳng DA, AE, EF, FD.
a) Chứng minh: EF là đường trung bình của tam giác ABC
b) Chứng minh: Các tứ giác DAEF; MNPQ là hình bình hành
c) Khi tam giác ABC vuông tại A thì các tứ giác DAEF; MNPQ là hình gì ? Chứng minh?
d)Tìm điều kiện của tam giác ABC để tứ giác MNPQ là hình vuông?

Gọi số ly trà sữa là x
=>Số ly trà đào là 210-x
Theo đề, ta có: 27000x=2*18000(210-x)
=>27000x-36000(210-x)=0
=>27000x-7560000+36000x=0
=>x=120
=>Số ly trà đào là 90 ly
 Giúp tớ với ạ nay tớ thi ấy=((
Giúp tớ với ạ nay tớ thi ấy=((


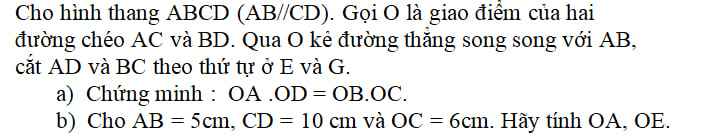

 giúp tớ với ạ. Cảm ơn mọi người rất nhiều ạ
giúp tớ với ạ. Cảm ơn mọi người rất nhiều ạ
Câu 3:
\(A=\dfrac{x^2+8x+16}{x^2-16}\)
a) Để phân thức \(A\) xác định thì \(x^2-16\ne0\Leftrightarrow x\ne\pm4\).
b) \(A=\dfrac{x^2+8x+16}{x^2-16}=\dfrac{x^2+2.x.4+4^2}{x^2-4^2}=\dfrac{\left(x+4\right)^2}{\left(x-4\right)\left(x+4\right)}=\dfrac{x+4}{x-4}\)
c) Với \(x=6\): \(A=\dfrac{6+4}{6-4}=5\).
Câu 4:
a) \(EF\) là đường trung bình của tam giác \(ABC\) suy ra \(EF \parallel AC\) và \(EF=\dfrac{1}{2}AC\).
\(GH\) là đường trung bình của tam giác \(CDA\) suy ra \(GH \parallel AC \) và \(GH=\dfrac{1}{2}AC\).
Suy ra \(EF \parallel GH\) và \(EF = GH\).
Suy ra tứ giác \(EFGH\) là hình bình hành.
Mà ta cũng có \(FG\) là đường trung bình của tam giác \(BCD\) suy ra \(FG \parallel BD\).
\(AC\perp BD\) (do tứ giác \(ABCD\) là hình thoi)
nên \(EF\perp FG\).
Do đó hình bình hành \(EFGH\) có một góc vuông nên nó là hình chữ nhật.
b) \(S_{EFGH}=EF.FG=\dfrac{1}{2}AC.\dfrac{1}{2}BD=10\left(cm^2\right)\)
