Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. Điểm biểu diễn các số: - 2; - 3; - 1 đều đặt ở bên trái điểm 0 nên các số này đều nhỏ hơn số 0;
Điểm biểu diễn các số 1; 2; 4 đều đặt ở bên phải điểm 0 nên các số này đều lớn hơn số 0.
b. Điểm – 2 và 2 nằm về hai phía của điểm 0 và cách đều điểm 0.
c. Chỉ đúng với trường hợp những điểm nằm về bên phải điểm 0. Đối với những điểm nằm về bên trái điểm 0 thì ngược lại: điểm nào ở xa gốc hơn thì biểu diễn số nhỏ hơn.

a)
Người đó dừng lại tại điểm 5.
Kết quả của hai hành động trên: 2+3=5
b)
Người đó dừng lại tại điểm -5.
Tổng 2+3=5. Số đối của \(\left( {2 + 3} \right)\) là \( - 5\).
Vậy người đó dừng lại điểm cùng giá trị với số đối của tổng (2+3).

Khi biểu diễn trục số:
Số nhỏ hơn 0 thì biểu diễn bên trái điểm 0
Số lớn hơn 0 thì biểu diễn bên phải điểm 0
----------------------------------------------
A. \(-4< 0\) biểu diễn bên trái điểm 0
B. Đúng
C. \(2>0\) nên được biểu diễn bên phải điểm 0, không nằm giữa 0 và -2
D. \(-5< 0\) nên biểu diễn theo chiều âm

a)
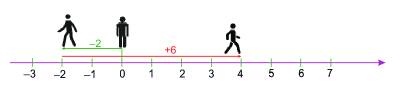
Người đó di chuyển về bên trái 2 đơn vị nên ta di chuyển sang trái 2 vạch (màu xanh) đến \( - 2\). Sau đó, sang phải 6 đơn vị nên ta di chuyển sang phải 6 vạch (màu đỏ) đến điểm +4. Vậy sau 2 lần di chuyển như trên, người đó dừng lại tại điểm +4.
Di chuyển sang trái 2 đơn vị là \(\left( { - 2} \right)\), sang phải 6 đơn vị là \(\left( { + 6} \right)\). Người đó dừng lại tại điểm +4 nên: \(\left( { - 2} \right) + \left( { + 6} \right) = + 4\).
b)
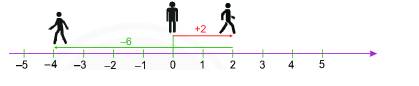
Người đó di chuyển về bên phải 2 đơn vị nên ta di chuyển sang phải 2 vạch. Sau đó, sang trái 6 đơn vị nên ta di chuyển sang trái 6 vạch đến điểm \( - 4\). Vậy sau 2 lần di chuyển như trên, người đó dừng lại tại điểm \( - 4\).
Di chuyển sang phải 2 đơn vị là \(\left( { + 2} \right)\), sang trái 6 đơn vị là \(\left( { - 6} \right)\). Người đó dừng lại tại điểm \( - 4\) nên: \(\left( { + 2} \right) + \left( { - 6} \right) = - 4\).

a) Người đó di chuyển về bên phải 4 đơn vị nên ta di chuyển sang phải 4 vạch. Sau đó, sang trái 4 đơn vị nên ta di chuyển sang trái 4 vạch đến điểm 0. Vậy sau 2 lần di chuyển như trên, người đó dừng lại tại điểm 0.
Di chuyển sang phải 4 đơn vị là \(\left( { + 4} \right)\), sang trái 4 đơn vị là \(\left( { - 4} \right)\). Người đó dừng lại tại điểm 0 nên: \(\left( { + 4} \right) + \left( { - 4} \right) = 0\)
b) Người đó di chuyển về bên trái 4 đơn vị nên ta di chuyển sang trái 4 vạch đến \( - 4\). Sau đó, sang phải 4 đơn vị nên ta di chuyển sang phải 4 vạch đến điểm 0. Vậy sau 2 lần di chuyển như trên, người đó dừng lại tại điểm 0.
Di chuyển sang trái 4 đơn vị là \(\left( { - 4} \right)\), sang phải 4 đơn vị là \(\left( { + 4} \right)\). Người đó dừng lại tại điểm 0 nên: \(\left( { - 4} \right) + \left( { + 4} \right) = 0\)

a) Biểu diễn các số –2; 0; 1; 2 trên trục số.
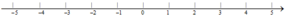
b) Ghi các số nguyên âm nằm giữa các số –4 và –1 trên trục số.
c) Trên trục số không có điểm nào biểu diễn số nguyên âm nằm giữa –2 và –1





Tham khảo:
Bước 1. Vẽ đường thẳng nằm ngang có mũi tên như sau:
Bước 2. Trên đường thẳng đánh dấu các điểm cách đều nhau. Chọn một điểm ở giữa biểu diễn cho số 0.
Bước 3. Về bên phải số 0 biểu diễn các số tăng dần từ trái sang phải lần lượt là 1; 2; 3; …
- Biểu diễn số 1: Ta di chuyển 1 đơn vị về bên phải số 0.
- Biểu diễn số 2: Ta di chuyển 2 đơn vị về bên phải số 0.
- Biểu diễn tương tự với các số nguyên dương còn lại.
Về bên trái số 0 biểu diễn các số -1; -2; -3; …
- Biểu diễn số - 1: Ta di chuyển 1 đơn vị về bên trái số 0.
- Biểu diễn số - 2: Ta di chuyển 2 đơn vị về bên phải số 0.
- Biểu diễn tương tự với các số nguyên âm còn lại.