
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


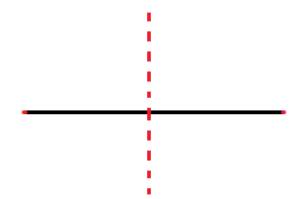
1. Thực hành gấp giấy: Vẽ đoạn thẳng trên tờ giấy, gấp tờ giấy theo một đường thẳng sao cho 2 đầu đoạn thẳng trùng nhau thì đường thẳng đó là một trục đối xứng.
+) Trục đối xứng của đoạn thẳng là đường thẳng thu được khi gấp giấy.
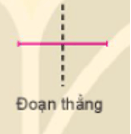
2.
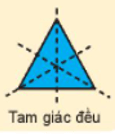
+) Trục đối xứng của tam giác đều là đường thẳng nối đỉnh của tam giác với trung điểm cạnh đối diện (có 3 trục đối xứng)
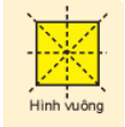
+) Trục đối xứng của hình vuông là đường chéo của hình vuông và hai đường thẳng đi qua trung điểm từng cặp cạnh đối diện của hình vuông (có 4 trục đối xứng)
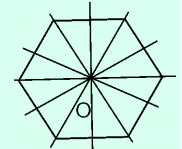
+) Trục đối xứng của lục giác đều là đường thẳng nối 1 đỉnh và tâm của lục giác đều (có 6 trục đối xứng).
a) Trục đối xứng của đoạn thẳng là đường thẳng thu được khi gấp giấy.
b)
+ Tam giác đều có 3 trục đối xứng là đường thẳng nối đỉnh của tam giác với trung điểm cạnh đối diện
+ Hình vuông có 4 trục đối xứng là đường chéo của hình vuông và hai đường thẳng đi qua trung điểm từng cặp cạnh đối diện của hình vuông
+ Hình lục giác đều có 6 trục đối xứng.

Ví dụ:
-Tập hợp các đồ vật (sách, bút) đặt trên bàn.
-Tập hợp học sinh lớp 6A.
-Tập hợp các số tự nhiên lớn hơn 7.
-Tập hợp các chữ cái trong hệ thống chữ cái Việt Nam.
1.1. Khái niệm tập hợp Tập hợp là một trong các khái niệm cơ bản của Toán học.
Khái niệm tập hợp không được định nghĩa mà chỉ được mô tả qua các ví dụ: Tập hợp các học sinh của một lớp học, tập hợp các cầu thủ của một đội bóng, tập hợp các cuốn sách trên một giá sách, tập hợp các số tự nhiên,... Mụn toán học nghiên cứu các tính chất chung của tập hợp, không phụ thuộc vào tính chất của các đối tượng cấu thành nên tập hợp được xem là cơ sở của Toán học hiện đại, và được gọi là lí thuyết tập hợp.
Khác với nhiều ngành Toán học khác mà sự phát triển là kết quả có được từ những cố gắng không mệt mỏi của nhiều tài năng toán học, cuộc đấu tranh với “vô cực” và tiếp theo đó, sự sáng tạo nên lí thuyết tập hợp là công trình của chỉ một người: Gioócgiơ − Căngtơ (Georg Cantor 1845 − 1918), nhà toán học Đức gốc Do Thái
. Các đối tượng cấu thành một tập hợp được gọi là các phần tử của tập hợp đó. Người ta thường kí hiệu các tập hợp bởi các chữ A, B, C, X, Y, Z,... và các phần tử của tập hợp bởi các chữ a, b, c, x, y, z, ...
Nếu a là một phần tử của tập hợp A thì ta viết a A (đọc là a thuộc tập hợp A). Nếu a không phải là một phần tử của tập hợp A thì ta viết a A (đọc là a không thuộc tập hợp A). Có hai cách xác định một tập hợp: z Cách thứ nhất là liệt kê tất cả các phần tử của tập hợp. Tập hợp A gồm bốn số tự nhiên 1, 3, 5, 7 được viết là: A = {1, 3, 5, 7}.
Tập hợp B gồm ba phần tử là các chữ a, b, c được viết là: B = {a, b, c}. z Cách thứ hai là nêu lên một tính chất chung của các phần tử của tập hợp, nhờ đó có thể nhận biết được các phần tử của tập hợp và các đối tượng không phải là những phần tử của nó. Chẳng hạn,
Ví dụ 1.1 : Cho tập hợp C các ước số của 8. Khi đó, các số 1, 2, 4, 8 là những phần tử của C, còn các số 3, 5, 6, 13 không phải là những phần tử của C. Người ta thường viết: C = {x : x là ước số của 8},

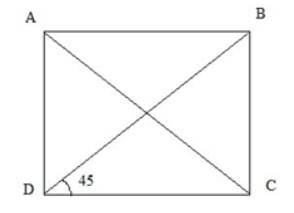
Góc tạo bởi một đường chéo và một cạnh hình vuông bằng 45 độ.
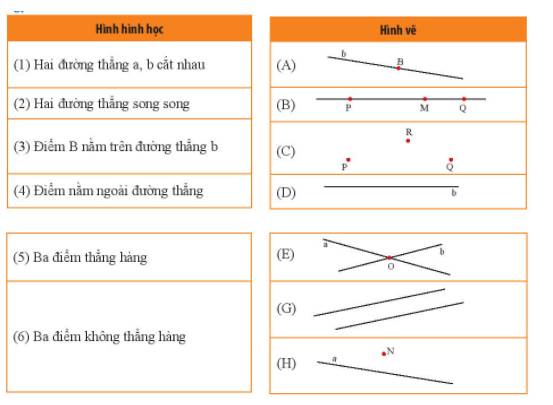
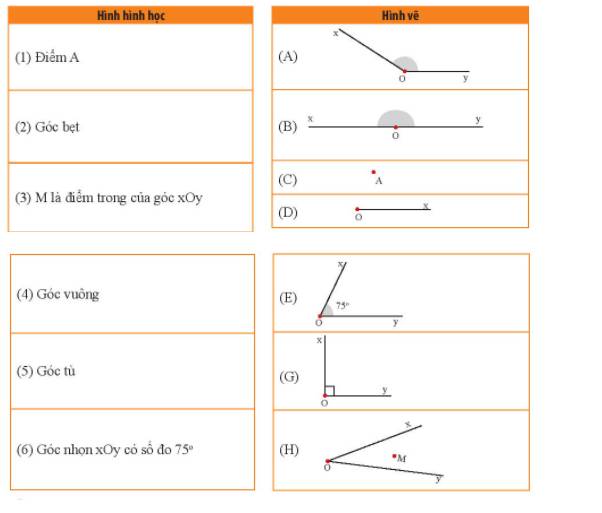

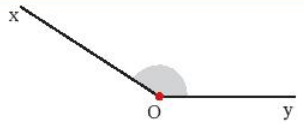



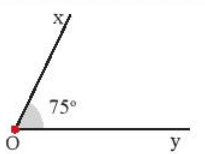
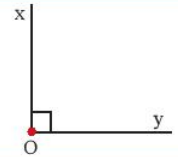
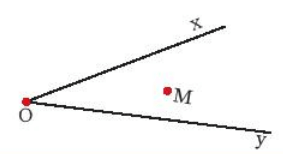

(1) - E (2) - G (3) - A
(4) - H (5) - B (6) - C