Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Năng lượng của electron ở trạng thái dừng n là \(E_n = -\frac{13,6}{n^2}.(eV)\)
\(hf_1 =\frac{hc}{\lambda_1}= E_3-E_1.(1) \)
\(hf_2 =\frac{hc}{\lambda_2}= E_5-E_2.(2) \)
Chia hai phương trình (1) và (2): \(\frac{\lambda_2}{\lambda_1}= \frac{E_3-E_1}{E_5-E_2}.(3)\)
Mặt khác: \(E_3-E_1 = 13,6.(1-\frac{1}{9}).\)
\(E_5-E_2 = 13,6.(\frac{1}{4}-\frac{1}{25}).\)
Thay vào (3) => \(\frac{\lambda_2}{\lambda_1}= \frac{800}{189}\) hay \(189 \lambda_2 = 800 \lambda_1.\)

Đáp án A
Ta có:
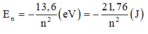
Bảng giá trị các mức năng lượng:
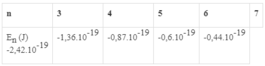
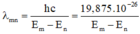 Áp dụng công thức:
Áp dụng công thức:
Khi đó:

Từ các kết quả trên cho thấy vạch phổ có bước sóng λ = 1875nm ứng với sự chuyển của electron giữa các quỹ đạo từ mức năng lượng ứng với n = 4 về mức năng lượng ứng với n = 3.

Đáp án D
– Khi electron chuyển từ quỹ đạo dừng M về quỹ đạo dừng L thì nguyên tử phát ra vạch quang phổ có bước sóng lớn nhất thuộc dãy Ban – me.
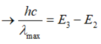
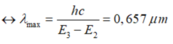
- Bước sóng ngắn nhất của vạch quang phổ thuộc dãy Ban – me là
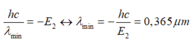
→ ∆λ = λmax - λmin = 0,657 – 0,365 = 0,292 µm.


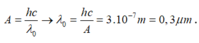
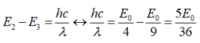
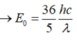
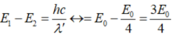
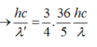
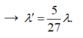


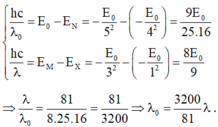
+ Bước sóng dài nhất ứng với sự chuyển từ mức năng lượng En về En – 1.
Bước sóng ngắn nhất ứng với sự chuyển mức năng lượng từ trạng thái En về trạng thái cơ bản.