Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án D.
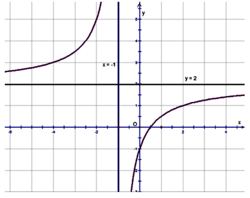
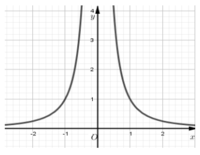
Hàm số tiệm cận ngang y = 2 nên loại B.
Đồ thị hàm số cắt trục tung tại điểm (0; -1) nên loại A, C.
Chọn B.
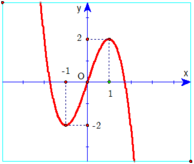
Để ý khi x = 0 thì y = 0 nên loại cả hai phương án A, C.
Dựa vào đồ thị, thấy đây là đồ thị của hàm bậc ba có hệ số a < 0 nên loại phương án D.
Chọn A.
Để ý khi x = 0 thì y = 1 nên loại phương án D.
Dựa vào đồ thị, thấy đây là đồ thị của hàm bậc ba có hệ số a > 0 nên loại hai phương án B và C.
Chọn A.
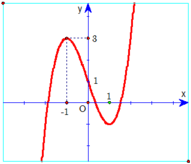
Để ý khi x = 0 thì y = 0 nên loại phương án D.
Dựa vào đồ thị, thấy đây là đồ thị của hàm bậc ba có hệ số a > 0 nên loại hai phương án B và C.
Đáp án D
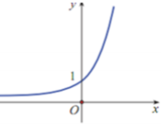
Dựa vào đồ thị hàm số ta thấy hàm số có tập xác định là ℝ và đồng biến trên ℝ
Do đó chỉ có đáp án D thỏa mãn.
Đáp án C.
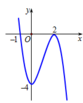
Hàm số cắt trục tung tại (0;-4) suy ra c = -4
Dựa vào đồ thị hàm số suy ra a < 0 và y’ = 0 có 2 nghiệm phân biệt
Đáp án A
Phương pháp:
Loại trừ từng đáp án.
Cách giải:
+) Đồ thị hàm số y = x4 có dạng là hình parabol ⇒ Loại phương án B
+) 
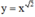có TXĐ: D = (0;+∞) ⇒ Loại phương án C
+) Đồ thị hàm số y = 2x luôn đồng biến trên R ⇒ Loại phương án D
Đáp án A.
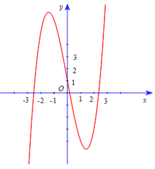
Đồ thị có a > 0, ab < 0, đồ thị đi qua (0; -1)
Hàm số y = x4 – 2x2 – 1 thỏa
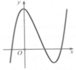
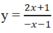
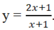
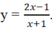
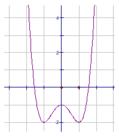
Đáp án C.
Ta thấy nhánh cuối bên phải của đồ thị hướng lên trên nên hệ số a > 0 => loại A.
Đồ thị hàm số có hai điểm cực trị => loại B, D do:
+ Hàm số y = x2 – 6x + 1 có 1 điểm cực trị
+ Hàm số y = x4 – 3x2 + 1 có 3 điểm cực trị