Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 6:(Sbt/25) Dùng tính chất cơ bản của phân thức để biến đổi mỗi cặp phân thức sau thành một cặp phân thức bằng nó và có cùng tử thức :
a) \(\dfrac{3}{x+2}\)và\(\dfrac{x-1}{5x}\)
Ta có:
\(\dfrac{3}{x+2}\) = \(\dfrac{3.\left(x-1\right)}{\left(x+2\right)\left(x-1\right)}\) = \(\dfrac{3x-3}{x^2+x-2}\)
\(\dfrac{x-1}{5x}\) = \(\dfrac{\left(x-1\right).3}{5x.3}\) =\(\dfrac{3x-3}{15x}\)
Vậy .....
b. \(\dfrac{x+5}{4x}\) và \(\dfrac{x^2-25}{2x+3}\)
Ta có:
\(\dfrac{x+5}{4x}\) = \(\dfrac{\left(x+5\right)\left(x-5\right)}{4x.\left(x-5\right)}\) = \(\dfrac{x^2-25}{4x^2-20x}\)
\(\dfrac{x^2-25}{2x+3}\)
Vậy .....

a ) \(\dfrac{x^2+3x+2}{3x+6}=\dfrac{\left(x+1\right)\left(x+2\right)}{3\left(x+2\right)}=\dfrac{x+1}{3}\) (1)
\(\dfrac{2x^2+x-1}{6x-3}=\dfrac{\left(2x-1\right)\left(x+1\right)}{3\left(2x-1\right)}=\dfrac{x+1}{3}\) (2)
Từ (1) ; (2) \(\Rightarrow\dfrac{x^2+3x+2}{3x+6}=\dfrac{2x^2+x-1}{6x-3}\) (đpcm)
b ) \(\dfrac{15x-10}{3x^2+3x-\left(2x+2\right)}=\dfrac{5\left(3x-2\right)}{\left(3x-2\right)\left(x+1\right)}=\dfrac{5}{x+1}\) (3)
\(\dfrac{5x^2-5x+5}{x^3+1}=\dfrac{5\left(x^2-x+1\right)}{\left(x+1\right)\left(x^2-x+1\right)}=\dfrac{5}{x+1}\) (4)
Từ (3) và (4) \(\Rightarrow\dfrac{15x-10}{3x^2+3x-\left(2x+2\right)}=\dfrac{5x^2-5x+5}{x^3+1}\) (đpcm)
a) \(\dfrac{x^2+3x+2}{3x+6}=\dfrac{x^2+x+2x+2}{3\left(x+2\right)}=\dfrac{\left(x^2+x\right)+\left(2x+2\right)}{3\left(x+2\right)}=\dfrac{x\left(x+1\right)+2\left(x+1\right)}{3\left(x+2\right)}=\dfrac{\left(x+1\right)\left(x+2\right)}{3\left(x+2\right)}=\dfrac{x+1}{3}\left(1\right)\) \(\dfrac{2x^2+x-1}{6x-3}=\dfrac{2x^2+2x-x-1}{3\left(2x-1\right)}=\dfrac{2x\left(x+1\right)-\left(x+1\right)}{3\left(2x-1\right)}=\dfrac{\left(2x-1\right)\left(x+1\right)}{3\left(2x-1\right)}=\dfrac{x+1}{3}\left(2\right)\) Từ (1)và (2)=> \(\dfrac{x^2+3x+2}{3x+6}=\dfrac{2x^2+x-1}{6x-3}\) b)\(\dfrac{15x-10}{3x^2+3x-\left(2x+2\right)}=\dfrac{5\left(3x-2\right)}{3x\left(x+1\right)-2\left(x+1\right)}=\dfrac{5\left(3x-2\right)}{\left(3x-2\right)\left(x+1\right)}=\dfrac{5}{x+1}\left(3\right)\) \(\dfrac{5x^2-5x+5}{x^3+1}=\dfrac{5\left(x^2-x+1\right)}{\left(x+1\right)\left(x^2-x+1\right)}=\dfrac{5}{x+1}\left(4\right)\) Từ (3) và (4) => \(\dfrac{15x-10}{3x^2+3x-\left(2x+2\right)}=\dfrac{5x^2-5x+5}{x^3+1}\)

\(\frac{x^2\left(x+2\right)}{x\left(x+2\right)^2}=\frac{x}{x+2}\Rightarrow\frac{x}{x+2}=\frac{x}{x+2}\)
\(\frac{3-x}{3+x}=\frac{x^2-6x+9}{9-x^2}\Rightarrow\frac{3-x}{3+x}=\frac{\left(3-x\right)^2}{\left(3-x\right)\left(3+x\right)}\Rightarrow\frac{3-x}{3+x}=\frac{3-x}{3+x}\)
\(\frac{x^3-4x}{10-5x}=\frac{-x^2-2x}{5}\Rightarrow-\frac{x\left(x-2\right)\left(x+2\right)}{5\left(x-2\right)}=\frac{-x^2-2x}{5}\)
\(\Rightarrow\frac{-x\left(x+2\right)}{5}=\frac{-x^2-2x}{5}\Rightarrow\frac{-x^2-2x}{5}=\frac{-x^2-2x}{5}\)
k nha bạn
sai rồi cái này là dùng định nghĩa 2 phân thức bằng nhau để chứng minh chúng bằng nhau mà
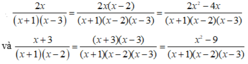
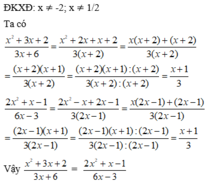
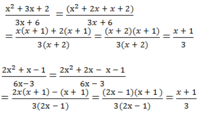
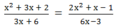
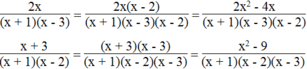
Hướng dẫn giải:
ĐKXĐ: x ≠ -1; x ≠ 2/3
Ta có: