Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(BD=AB+AD=4+5=9\left(cm\right)\)
\(\Delta ABC\) và \(\Delta CBD\) có:
\(\frac{AB}{BC}=\frac{BC}{BD}\left(=\frac{2}{3}\right)\)
Góc B chung
\(\Rightarrow\Delta ABC\infty\Delta CBD\left(c.g.c\right)\Rightarrow\hept{\begin{cases}\widehat{ACB}=\widehat{D}\\\frac{AB}{CB}=\frac{AC}{CD}\left(1\right)\end{cases}}\)
b, Từ (1) thay số vào: \(\frac{4}{6}=\frac{5}{CD}\Rightarrow CD=7,5\left(cm\right)\)
c, \(\widehat{BAC}=\widehat{D}+\widehat{ACD}=2\widehat{D}=2\widehat{ACB}\)

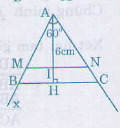
Trên hai cạnh Ax, Ay của góc \(\widehat{xAy}\) đặt AM = 4 đơn vị, AN = 5 đơn vị. Kẻ đường cao AH của \(\Delta\)AMN.
Trên tia AI lấy điểm H sao cho AH = 6cm, qua H vẽ đường song song với MN cắt Ax, Ay lần lượt tại B và C => \(\Delta\)ABC thỏa mãn điều kiện để bài
Thật vậy:
MN // BC => \(\Delta\)AMN ∽ \(\Delta\)ABC => \(\dfrac{AM}{AN}=\dfrac{AB}{AC}=\dfrac{4}{5}\)
Vậy AH \(\perp\) BC, AH = 6cm => AH là đường cao.




A B C D