

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



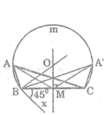
- Dựng đoạn thẳng AB = 3cm
- vẽ tia Bx sao cho góc (CBx) = 45 °
- Dựng trung điểm M của BC
- Dựng đường trung trực của BC (qua M)
- Dựng tia vuông góc với Bx tại B ,cắt đường trung trực của BC tại O
- Dựng cung tròn BmC bán kính OB là cung chứa góc 45 ° vẽ trên đoạn BC
- Dựng đường tròn tâm M bán kính 2,5cm cắt cung BmC lần lượt tại A và A’
- Nối AB , AC (hoặc A’B , A’C) ta có: ∆ ABC ( ∆ A’BC) có BC = 3cm , góc A = 45 ° (hoặc góc (A' ) =45°) và trung tuyến AM =2,5cm

Bài 2:
\(\cos60^0=\dfrac{28^2+35^2-BC^2}{2\cdot28\cdot35}\)
\(\Leftrightarrow2009-BC^2=980\)
hay \(BC=7\sqrt{21}\left(cm\right)\)

Bài 2:
Xét \(\Delta ABC\)có \(\widehat{A}=90^o\)và\(AH\perp BC\)
\(\Rightarrow AH^2=HB.HC\)(Hệ thức lượng)
\(AH^2=25.64\)
\(AH=\sqrt{1600}=40cm\)
Xét \(\Delta ABH\)có\(\widehat{H}=90^o\)
\(\Rightarrow\tan B=\frac{AH}{BH}\)\(=\frac{40}{25}=\frac{8}{5}\)
\(\Rightarrow\widehat{B}\approx58^o\)
Xét \(\Delta ABC\)có \(\widehat{A}=90^o\)
\(\Rightarrow\widehat{B}+\widehat{C}=90^o\)
\(58^o+\widehat{C}=90^o\)
\(\Rightarrow\widehat{C}\approx90^o-58^o\)
\(\widehat{C}\approx32^o\)

Hướng dẫn làm bài:
Dựng BC = 4cm và đường thẳng (d) song song với BC và cách BC một khoảng là 1cm
Tâm O của đường tròn nội tiếp ∆ABC là giao điểm của đường thẳng (d) với cung chứa góc 90° + 60° : 2 = 120° dựng trên đoạn BC cố định
Qua B và C vẽ các tiếp tuyến với (O), chúng cắt nhau tại A. Tam giác ABC là tam giác phải dựng
Dựng BC = 4cm và đường thẳng (d) song song với BC và cách BC một khoảng là 1 cm.
Tâm O của đường tròn nội tiếp tam giác ABC là giao điểm của đường thẳng (d) với cung chứa góc 90o + 60o : 2 = 120o dựng trên đoạn BC cố định.
Qua B và C vẽ các tiếp tuyến với (O), chúng cắt nhau tại A.
Tam giác ABC là tam giác cần dựng.

a) \(\left(sinA+cosA\right)^2=sin^2A+cos^2A+2sinAcosA=1+2sinAcosA\)
vì tam giác \(ABC\)nhọn nên \(0^o< \widehat{A}< 90^o\)nên \(sinA>0,cosA>0\Rightarrow2sinAcosA>0\)
nên \(\left(sinA+cosA\right)^2>1\Leftrightarrow sinA+cosA>1\)do \(sinA>0,cosA>0\).
b) Kẻ đường cao \(AH\).
Đặt \(HB=x\Rightarrow HC=a-x\).
Xét tam giác \(AHB\)vuông tại \(H\): \(AH=HB.tan\widehat{ABH}=xtan45^o=x\)
Xét tam giác \(AHC\)vuông tại \(H\): \(AH=HCtan\widehat{ACH}=\left(a-x\right)tan60^o=\sqrt{3}\left(a-x\right)\)
Ta có: \(x=\sqrt{3}\left(a-x\right)\Leftrightarrow x=\frac{\sqrt{3}}{1+\sqrt{3}}a\)
\(S_{ABC}=\frac{1}{2}AH.BC=\frac{1}{2}\frac{\sqrt{3}}{1+\sqrt{3}}a.a=\frac{3-\sqrt{3}}{4}a^2\).