
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Có \(\left(\sqrt{17-3\sqrt{32}}+\sqrt{17+3\sqrt{32}}\right)^2\)
\(=\left(\sqrt{17-3\sqrt{32}}\right)^2+2\left(\sqrt{17-3\sqrt{32}}\right)\left(\sqrt{17+3\sqrt{32}}\right)\)\(+\left(\sqrt{17=3\sqrt{32}}\right)^2\)
\(=17-3\sqrt{32}+2\sqrt{\left(17-3\sqrt{32}\right)\left(17+3\sqrt{32}\right)}\)\(+17+3\sqrt{32}\)
\(=34+2\sqrt{17^2-9.32}\)
\(=34+2\sqrt{289-288}\)
\(=34+2\sqrt{1}=34+2=36\)
\(\Rightarrow\sqrt{17-3\sqrt{32}}+\sqrt{17+3\sqrt{32}}\)
\(=\sqrt{36}=6\)
(Vì có \(\hept{\begin{cases}\sqrt{17-3\sqrt{32}}\ge0\\\sqrt{17+3\sqrt{32}}\ge0\end{cases}}\)nên \(\sqrt{17-3\sqrt{32}}+\sqrt{17+3\sqrt{32}}\ge0\))

4x^2 - 7x -2 = 4x^2 - 8x + x - 2 = 4x(x - 2) + (x - 2) = (x -2)(4x + 1)

\(\sqrt{7+4\sqrt{3}}=\sqrt{\left(2+\sqrt{3}\right)^2}=2+\sqrt{3}\)
\(\sqrt{8-2\sqrt{12}}=\sqrt{\left(\sqrt{6}-\sqrt{2}\right)^2}=\left|\sqrt{6}-\sqrt{2}\right|=\sqrt{6}-\sqrt{2}\)
\(\sqrt{21+6\sqrt{6}}=\sqrt{\left(3\sqrt{2}-\sqrt{3}\right)^2}=\left|3\sqrt{2}-\sqrt{3}\right|=3\sqrt{2}-\sqrt{3}\)
\(\sqrt{15-6\sqrt{6}}=\sqrt{\left(3-\sqrt{6}\right)^2}=\left|3-\sqrt{6}\right|=3-\sqrt{6}\)
\(\sqrt{29-12\sqrt{5}}=\sqrt{\left(2\sqrt{5}-3\right)^2}=\left|2\sqrt{5}-3\right|=2\sqrt{5}-3\)
\(\sqrt{41+12\sqrt{5}}=\sqrt{\left(6+\sqrt{5}\right)^2}=6+\sqrt{5}\)

\(7,=\left(\sqrt{x}\right)^2+2\cdot2\sqrt{x}+2^2=\left(\sqrt{x}+2\right)^2\\ 8,=\left(\sqrt{x}\right)^2-2\cdot3\sqrt{x}+3^2=x-6\sqrt{x}+9\\ 9,=\sqrt{x^3}+\sqrt{y^3}=\left(\sqrt{x}+\sqrt{y}\right)\left(x-\sqrt{xy}+y\right)\\ 10,=\sqrt{x^3}-\sqrt{y^3}=\left(\sqrt{x}-\sqrt{y}\right)\left(x+\sqrt{xy}+y\right)\\ 11,=\sqrt{x^3}+1^3=\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)\\ 12,=\sqrt{x^3}-2^3=\left(\sqrt{x}-2\right)\left(x+2\sqrt{x}+4\right)\)
7: \(x+4\sqrt{x}+4=\left(\sqrt{x}+2\right)^2\)
8: \(\left(\sqrt{x}-3\right)^2=x-6\sqrt{x}+9\)
9: \(x\sqrt{x}+y\sqrt{y}=\left(\sqrt{x}+\sqrt{y}\right)\left(x-\sqrt{xy}+y\right)\)

7) \(x+4\sqrt{x}+4=\left(\sqrt{x}\right)^2+2\sqrt{x}.2+2^2=\left(\sqrt{x}+2\right)^2\)
8) \(\left(\sqrt{x}-3\right)^2=\left(\sqrt{x}\right)^2-2.\sqrt{x}.3+3^2=x-6\sqrt{x}+9\)
9) \(x\sqrt{x}+y\sqrt{y}=\sqrt{x^3}+\sqrt{y^3}=\left(\sqrt{x}+\sqrt{y}\right)\left(x-\sqrt{xy}+y\right)\)
10) \(x\sqrt{x}-y\sqrt{y}=\sqrt{x^3}-\sqrt{y^3}=\left(\sqrt{x}-\sqrt{y}\right)\left(x+\sqrt{xy}+y\right)\)
11) \(x\sqrt{x}+1=\sqrt{x^3}+1^3=\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)\)
12) \(x\sqrt{x}-8=\sqrt{x^3}-2^3=\left(\sqrt{x}-2\right)\left(x+2\sqrt{x}+4\right)\)



9) \(x-1=\left(\sqrt{x}\right)^2-1=\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)\)
10) \(x\sqrt{x}-1=\sqrt{x^3}-1=\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)\)
11) \(x-2\sqrt{x}-63=\left(x-2\sqrt{x}+1\right)-64=\left(\sqrt{x}-1\right)^2-8^2=\left(\sqrt{x}-1-8\right)\left(\sqrt{x}-1+8\right)=\left(\sqrt{x}-9\right)\left(\sqrt{x}+7\right)\)
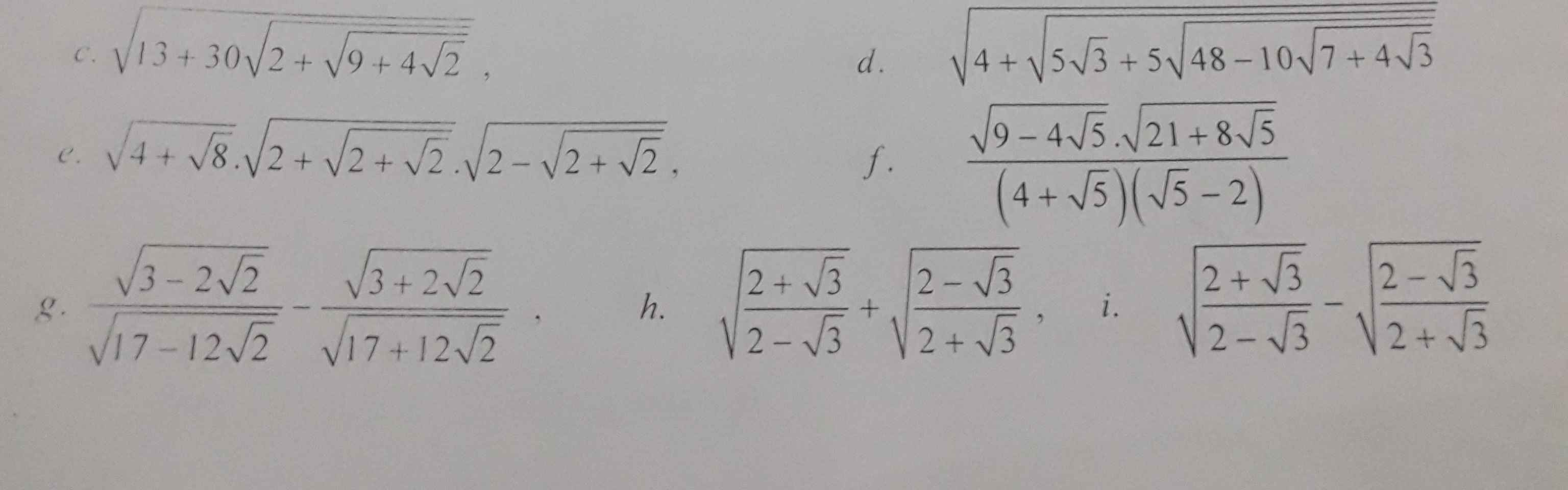





h: Ta có: \(\sqrt{\dfrac{2+\sqrt{3}}{2-\sqrt{3}}}+\sqrt{\dfrac{2-\sqrt{3}}{2+\sqrt{3}}}\)
\(=2+\sqrt{3}+2-\sqrt{3}\)
=4