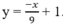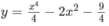Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
![]() (*)
(*)
Đặt ![]()
Yêu cầu bài toán trở thành: Tìm m để phương trình ![]() có nghiệm
có nghiệm ![]()
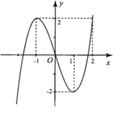
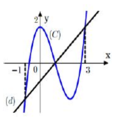
Từ đồ thị đã cho, ta suy ra đồ thị của hàm số ![]()
Từ đó ta có kể quả thỏa mãn yêu cầu bài toán ![]()

a)
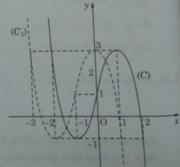
b) Tịnh tiến (C) song song với trục Ox sang trái 1 đơn vị, ta được đồ thị (C1) của hàm số.
y = f(x) = − ( x + 1 ) 3 + 3(x + 1) + 1 hay f(x) = − ( x + 1 ) 3 + 3x + 4 (C1)
Lấy đối xứng (C1) qua trục Ox, ta được đồ thị (C’) của hàm số y = g(x) = ( x + 1 ) 3 − 3x – 4
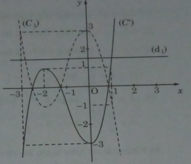
c) Ta có: ( x + 1 ) 3 = 3x + m (1)
⇔ ( x + 1 ) 3 − 3x – 4 = m – 4
Số nghiệm của phương trình (1) là số giao điểm của hai đường :
y = g(x) = ( x + 1 ) 3 − 3x – 4 (C’) và y = m – 4 (d1)
Từ đồ thị, ta suy ra:
+) m > 5 hoặc m < 1: phương trình (1) có một nghiệm.
+) m = 5 hoặc m = 1 : phương trình (1) có hai nghiệm.
+) 1 < m < 5 , phương trình (1) có ba nghiệm.
d) Vì (d) vuông góc với đường thẳng:
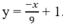
nên ta có hệ số góc bằng 9.
Ta có: g′(x) = 3 ( x + 1 ) 2 – 3
g′(x) = 9 ⇔ 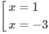
Có hai tiếp tuyến phải tìm là:
y – 1 = 9(x – 1) ⇔ y = 9x – 8;
y + 3 = 9(x + 3) ⇔ y = 9x + 24.

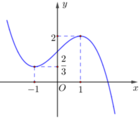
a) Tập xác định: D = R
y′=0 ⇔ 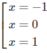
Hàm số đồng biến trên mỗi khoảng (-1; 0) và (1; + ∞ )
Hàm số nghịch biến trên mỗi khoảng (− ∞ ; −1); (0; 1)
Hàm số đạt cực đại tại x = 0; y C Đ = 0
Hàm số đạt cực tiểu tại x = 1 hoặc x = -1; y C T = −2
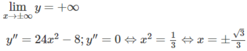
Đồ thị có hai điểm uốn:
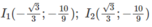
Bảng biến thiên:
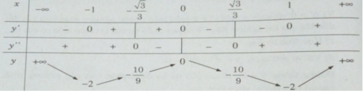
Đồ thị:
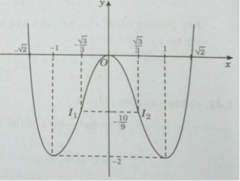
Đồ thị cắt trục hoành tại:
b) Ta có: x 2 | x 2 − 2| = m
⇔ 2 x 2 | x 2 − 2| = 2m
⇔|2 x 2 ( x 2 − 2)| = 2m
⇔|2 x 4 − 4 x 2 | = 2m
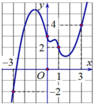
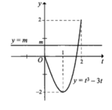
Từ đồ thị hàm số y = 2 x 4 – 4 x 2 có thể suy ra đồ thị của hàm số y = |2 x 4 − 4 x 2 | như sau:
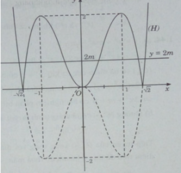
Phương trình: |2 x 4 − 4 x 2 | = 2m có 6 nghiệm phân biệt khi và chỉ khi đường thẳng y = 2m có 6 nghiệm phân biệt với đồ thị (H)
⇔ 0 < 2m < 2
⇔ 0 < m < 1

Số nghiệm của phương trình x 3 + 3 x 2 + 1 = m 2 bằng số giao điểm của đồ thị (C) và đường thẳng y = m/2.
Từ đồ thị ta có:
+ Đường thẳng cắt đồ thị tại 1 điểm khi và chỉ khi :
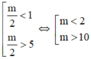
⇒ phương trình có 1 nghiệm.
+ Để đường thẳng cắt đồ thị tại 2 điểm phân biệt khi và chỉ khi :
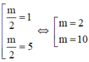
⇒ Phương trình có hai nghiệm.
+ Với 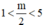 ⇔ 2 < m < 10.
⇔ 2 < m < 10.
⇒ Đường thẳng cắt đồ thị hàm số tại 3 điểm
⇒ Phương trình có ba nghiệm phân biệt.

a) Học sinh tự giải
b) 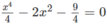
⇔ x 4 − 8 x 2 − 9 = 0
⇔ ( x 2 + 1)( x 2 − 9) = 0
⇔ 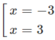
(C) cắt trục Ox tại x = -3 và x = 3
Ta có: y′ = x 3 − 4x
Phương trình tiếp tuyến của (C) tại điểm có hoành độ x = 3 và x = -3 lần lượt là:
y = y′(3)(x – 3) và y = y′(−3)(x + 3)
Hay y = 15(x – 3) và y = −15(x + 3)
c) 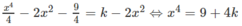
Từ đó, ta có:
k = −9/4: (C) và (P) có một điểm chung là (0; −9/4)
k > −9/4: (C) và (P) có hai giao điểm.
k < −9/4: (C) và (P) không cắt nhau.