Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

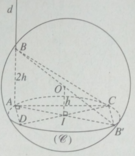
Diện tích tam giác BCD bằng:
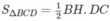
Diện tích này lớn nhất khi AI // CD.

Đáp án B.
Xác suất để xạ thủ thứ nhất bắn không trúng bia là: 1 − 1 2 = 1 2
Xác suất để xạ thủ thứ hai bắn không trúng bia là: 1 − 1 3 = 2 3
Gọi biến cố A: Có ít nhất một xạ thủ không bắn trúng bia . Khi có biến cố A có 3 khả năng xảy ra:
* Xác suất người thứ nhất bắn trúng bia, người thứ hai không bắn trúng bia là 1 2 . 2 3 = 1 3
* Xác suất người thứ nhất không bắn trúng bia, người thứ hai bắn trúng bia là 1 2 . 1 3 = 1 6
* Xác suất cả hai người đều bắn không trúng bia là 1 2 . 2 3 = 1 3

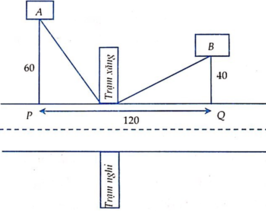
Gọi gia tốc trong chuyển động nhanh dần đều của chất điểm A là a thì vận tốc của A là v A ( t ) = a t

Quãng đường A chuyển động được trong 8 giây đầu là
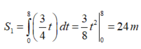
Thời gian A chuyển động đều cho đến lúc gặp B là 12 giây.
Quãng đường A đi được trong chuyển động đều là S 2 = 6 . 12 = 72 m
Quãng đường A đi được từ lúc xuất phát đến lúc gặp B là
S = S 1 + S 2 = 72 + 24 = 96
Gọi gia tốc của B là b thì vận tốc của B là v B ( t ) = b t
Quãng đường B đi được từ lúc xuất phát đến lúc gặp A là 96 m.
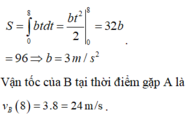
Đáp án C

Gọi sự kiện A là vị trí này có nước ngầm, sự kiện B là máy báo đúng.
Ta có:
P(A) = 7/10 (vì cứ 10 địa điểm bị nghi vấn thì có 7 vị trí là có nước ngầm)
P(B|A) = 0.85 (vị trí có nước ngầm máy báo đúng với xác suất 0.85)
P(~B|~A) = 0.9 (vị trí không có nước ngầm máy báo sai với xác suất 0.1)
`(a)` Ta cần tính xác suất P(A|B), tức là vị trí này có nước ngầm khi máy báo đúng.
Theo công thức Bayes, ta có:
P(A|B) = P(B|A) * P(A) / P(B)
Trong đó:
P(B) = P(B|A) * P(A) + P(B|~A) * P(~A) (theo định lý xác suất toàn phần)
P(~A) = 1 - P(A) (vì chỉ có hai khả năng: có nước ngầm hoặc không có nước ngầm)
Thay giá trị vào ta được:
P(B) = P(B|A) * P(A) + P(B|~A) * P(~A) = 0.85 * 7/10 + 0.9 * 3/10 = 0.865
P(A|B) = P(B|A) * P(A) / P(B) = 0.85 * 7/10 / 0.865 ≈ 0.692
Vậy xác suất vị trí này có nước ngầm khi máy báo đúng là khoảng 69.2%.
`(b)` Ta cần tính xác suất P(B), tức là máy báo đúng.
Theo công thức Bayes, ta có:
P(B) = P(B|A) * P(A) + P(B|~A) * P(~A)
Thay giá trị vào ta được:
P(B) = P(B|A) * P(A) + P(B|~A) * P(~A) = 0.85 * 7/10 + 0.1 * 3/10 = 0.655
Vậy xác suất máy báo đúng là khoảng 65.5%.