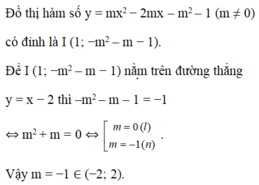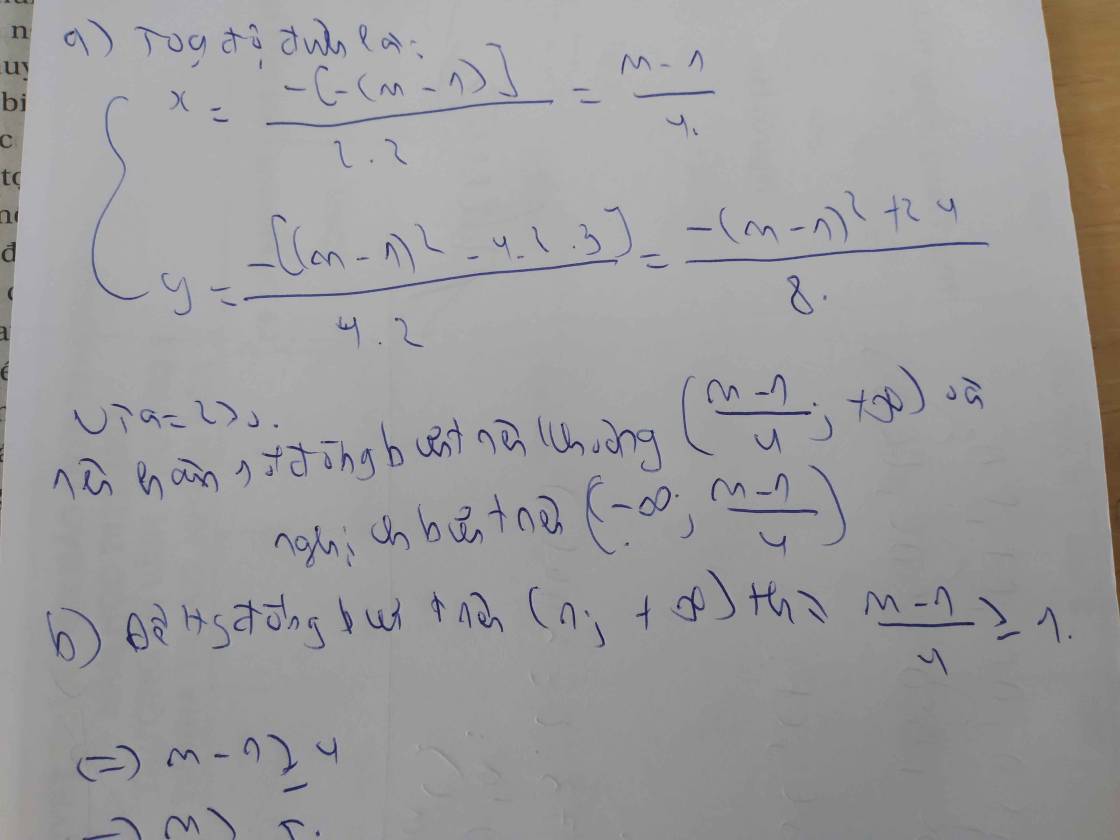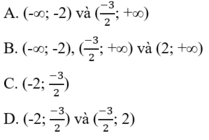Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Tọa độ đỉnh là:
\(\left\{{}\begin{matrix}x=\dfrac{-6}{2\cdot4}=\dfrac{-6}{8}=\dfrac{-3}{4}\\y=-\dfrac{6^2-4\cdot4\cdot\left(-5\right)}{4\cdot4}=-\dfrac{29}{4}\end{matrix}\right.\)
Bảng biến thiên là:
| x | -\(\infty\) -3/4 +\(\infty\) |
| y | -\(\infty\) -29/4 +\(\infty\) |

b: Hàm số đồng biến khi x>-3/4; nghịch biến khi x<-3/4
GTNN của hàm số là y=-29/4 khi x=-3/4

a: Tọa độ đỉnh là:
\(\left\{{}\begin{matrix}x=\dfrac{-10}{2\cdot\left(-3\right)}=\dfrac{10}{6}=\dfrac{5}{3}\\y=-\dfrac{10^2-4\cdot\left(-3\right)\cdot\left(-4\right)}{4\cdot\left(-3\right)}=\dfrac{13}{3}\end{matrix}\right.\)
Bảng biến thiên:
| x | -\(\infty\) 5/3 +\(\infty\) |
| y | +\(\infty\) 13/3 -\(\infty\) |

b: Hàm số đồng biến khi x<5/3; nghịch biến khi x>5/3
Giá trị nhỏ nhất là y=13/3 khi x=5/3

Pt hoành độ giao điểm:
\(\sqrt{2x^2-2x-m}-x-1=0\)
\(\Leftrightarrow\sqrt{2x^2-2x-m}=x+1\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge-1\\2x^2-2x-m=x^2+2x+1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge-1\\x^2-4x-1=m\left(1\right)\end{matrix}\right.\)
Bài toán thỏa mãn khi (1) có 2 nghiệm pb \(x\ge-1\)
Từ đồ thị hàm \(y=x^2-4x-1\) ta thấy \(-5< m\le4\)

tròi oi a viết chữ xấu wá đi à, đọc bài của a mà đau mắt wá

Tại x = –2; –1; 0; 1; 2 thì y = 2
+) Đồ thị của hàm số y = 2 là đường thẳng song song với trục hoành và cắt trục tung tại điểm (0; 2).
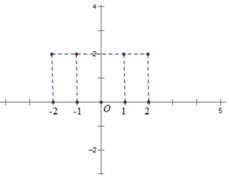

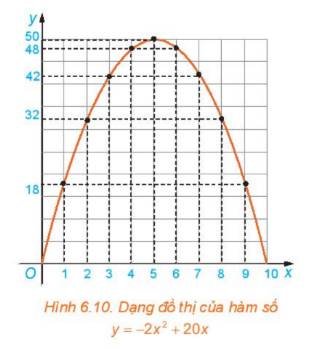
a) Ta có đồ thị hàm số \(y = - 2{x^2}\)
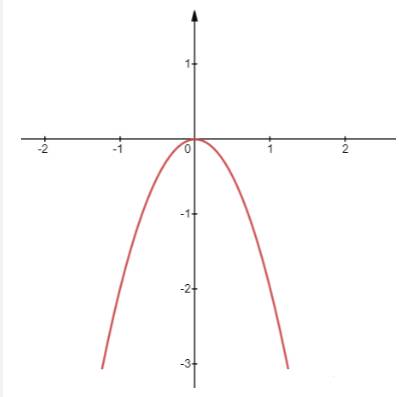
Nhìn vào 2 đồ thị, ta thấy dạng đồ thị của hàm số \(y = - 2{x^2} + 20x\)giống với dạng đồ thị \(y = - 2{x^2}\)
b) Tọa độ điểm cao nhất là \(\left( {5;50} \right)\)
c) Ta có: \(S(x) = y = - 2{x^2} + 20x = - 2({x^2} - 10x) = - 2({x^2} - 2.5.x + 25) + 50 = - 2{(x - 5)^2} + 50\)
\({(x - 5)^2} \ge 0 \Rightarrow - 2{(x - 5)^2} + 50 \le 50 \Rightarrow S(x) \le 50\)
Do đó diện tích lớn nhất của mảnh đất rào chắn là 50 \(({m^2})\) khi x = 5.

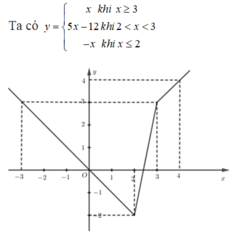
Cách 1. Lập bảng xét dấu.
Cách 2. f(x) không xác định khi x = 2 và 2 ∈ ((-3)/2; +∞) nên A sai. Dễ thấy x = (-7)/4 thì x 2 – 4 < 0; x – 2 < 0; 2x + 3 < 0 ⇒ f(x) < 0, vì vậy C và D sai.
Đáp án: B