Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có nhận xét: trong cùng một bảng điều tra; khi 2 giá trị có tần số bằng nhau thì tần suất của chúng cũng bằng nhau và ngược lại
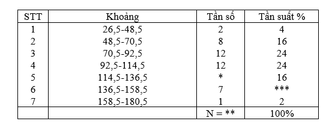
Ta thấy; lớp thứ 5 và lớp thứ 2 có cùng tần suất nên tần số của chúng là bằng nhau.
Do đó; số cần tìm là : 8
Chọn C.

Cách 1: tổng các tần suất là 100 % nên giá trị cần tìm là:
100- ( 4+ 16+24+24+16+2)= 14%
Cách 2: *** = 7 50 . 100 % = 14%
Chọn C

a) Năm 2019:
+) Số trung bình: \(\overline x = \frac{{54 + 22 + 24 + 30 + 35 + 40 + 31 + 29 + 29 + 37 + 40 + 31}}{{12}} = 33,5\)
+) Phương sai \({S^2} = \frac{1}{{12}}\left( {{{54}^2} + {{22}^2} + ... + {{31}^2}} \right) - 33,{5^2} = 67,25\) => Độ lệch chuẩn \(S = \sqrt {{S^2}} \approx 8,2\)
+) Khoảng tứ phân vị: \({\Delta _Q} = {Q_3} - {Q_1}\)
Sắp xếp mẫu số liệu theo thứ tự không giảm: 22, 24, 29, 29, 30, 31, 31, 35, 37, 40, 40, 54
\({Q_2} = {M_e} = \frac{1}{2}(31 + 31) = 31\)
\({Q_1}\) là trung vị của nửa số liệu: 22, 24, 29, 29, 30, 31. Do đó \({Q_1} = 29\)
\({Q_3}\) là trung vị của nửa số liệu: 31, 35, 37, 40, 40, 54. Do đó \({Q_3} = 38,5\)
\( \Rightarrow {\Delta _Q} = 38,5 - 29 = 9,5\)
Năm 2020:
+) Số trung bình: \(\overline x = 34,5\)
+) Phương sai \({S^2} = \frac{1}{{12}}\left( {{{45}^2} + {{28}^2} + ... + {{37}^2}} \right) - 34,{5^2} = 15,75\) => Độ lệch chuẩn \(S = \sqrt {{S^2}} \approx 3,97\)
+) Khoảng tứ phân vị: \({\Delta _Q} = {Q_3} - {Q_1}\)
Sắp xếp mẫu số liệu theo thứ tự không giảm: 28, 31, 32, 33, 33, 34, 34, 35, 35, 37, 37, 45.
\({Q_2} = {M_e} = \frac{1}{2}(34 + 34) = 34\)
\({Q_1}\) là trung vị của nửa số liệu: 28, 31, 32, 33, 33, 34. Do đó \({Q_1} = 32,5\)
\({Q_3}\) là trung vị của nửa số liệu: 34, 35, 35, 37, 37, 45. Do đó \({Q_3} = 36\)
\( \Rightarrow {\Delta _Q} = 36 - 32,5 = 3,5\)
b) Nhận xét:
So sánh số trung bình: số lượng bán ra trung bình theo tháng không tăng nhiều so với năm trước (tăng 1)
So sánh độ lệch chuẩn: Số lượng xe bán ra năm 2020 không có sự chênh lệch quá nhiều giữa các tháng.
=> Tác động của chiến lược: Số lượng xe bán ra tăng ít, nhưng đồng đều giữa các tháng.

Để cửa hàng có lãi thì lợi nhuận lớn hơn 0, suy ra \(I > 0 \Leftrightarrow - 3{x^2} + 200x - 2325 > 0\)
Tam thức \(I = - 3{x^2} + 200x - 2325\) có \(\Delta = 12100 > 0\), có hai nghiệm phân biệt \({x_1} = 15;{x_2} = \frac{{155}}{3}\) và có \(a = - 3 < 0\)
Ta có bảng xét dấu như sau:
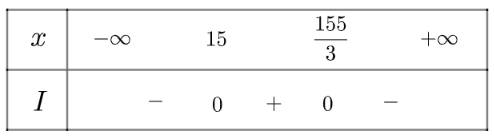
Vậy ta thấy cửa hàng có lợi nhuận khi \(x \in \left( {15;\frac{{155}}{3}} \right)\) (kg)

Bảng số liệu có 7 giá trị, sắp các giá trị theo thứ tự không giảm ta có:
650, 670, 690, 720, 840, 2500, 3000.
Vì số phần tử = 7 là số lẻ nên số trung vị là Me = 720 (số chính giữa của dãy).
Ý nghĩa:
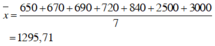
Số trung bình này chênh lệch quá lớn so với các số liệu nên không đại diện được cho các số liệu.
Trong trường hợp này, số trung vị nên được chọn làm giá trị đại diện cho mức lương.

a) Thu nhập trung bình của thành viên trong công ty là
\(\bar X = \frac{{20.1 + 4.5}}{6} = \frac{{40}}{6} \approx 6,67\)
Vậy thu nhập trung bình của các thành viên là 6,67 triệu đồng.
b) Ta thấy rõ ràng thu nhập của giám đốc cao hơn thu nhập trung bình rất nhiều (khoảng 13,3 triệu), còn thu nhập của mỗi nhân viên thì gần với thu nhập trung bình hơn (khoảng 2,67 triệu). Như thế, thu nhập trung bình không phản ánh đúng thu nhập của nhân viên công ty.
Chú ý
Công ty có 6 người thì cần tính thu nhập trung bình của 6 người.

Dễ thấy: Hoa hồng nhung là loại hoa bán được nhiều nhất trong dịp năm nay, do đó cửa hàng nên nhập loại hoa này nhiều nhất để bán vào dịp 14 tháng 2 năm sau.

Từ năm 1991 đến hết năm 2000 là có 10 năm. Do đó kích thước mẫu là 10.
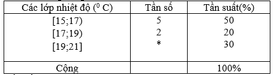
Dựa vào bảng thống kê ta có: n1= 5; n2= 2
Do đó n3= N – n1- n2 = 10- 5-2=3
Chọn B.
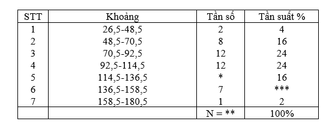
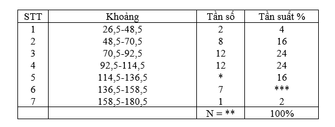
Cách 1: Kích thước mẫu bằng tổng các tần số. Nên kích thước mẫu cần tìm là
N= 2+ 8+ 12+ 12+ 8+ 7+1= 50
Cách 2: Theo đề bài thì ta đang điều tra doanh thu của 50 cửa hàng nên kích thước mẫu là 50.
Chọn A