Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án: B
Sử dụng các công thức của bài toán điện dung của tụ điện thay đổi.
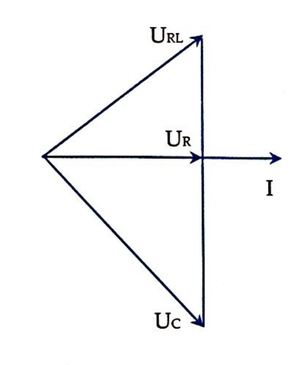
Điều chỉnh C để điện áp hiệu dụng hai đầu tụ đạt giá trị cực đại thì uRL vuông pha với u.
Ta có giản đồ véc tơ như hình bên
Khi đó u R L 2 U 0 R L 2 + u 2 U 0 2 = 1 ⇔ 50 2 . 6 U 0 R L 2 + 150 2 . 6 U 0 2 = 1 (1)
Mặt khác, từ hệ thức lượng trong tam giác vuông ta có:
1
U
0
R
L
2
+
1
U
0
2
=
1
U
0
R
2
=
1
150
2
.
2
(2)
Giải (1) và (2) ta thu được U 0 2 = 180000 ⇒ U 0 = 300 2 ⇒ U = 300 (V)

Đáp án B
Phương pháp giải: Sử dụng các công thức của bài toán điện dung của tụ điện thay đổi.
Điều chỉnh C để điện áp hiệu dụng hai đầu tụ đạt giá trị cực đại thì uRL vuông pha với u.


Đáp án A
Phương pháp: Sử dụng giản đồ vecto
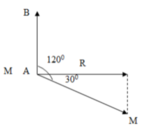
Cách giải:
Có:
Z C R = 1 3 ⇒ R = 3 Z C ⇒ Z L = 4 Z C
⇒ Z C = 30 Ω = 1 ω C ⇒ C = 10 - 3 3 π F

+ \(U_{AM}=I.Z_{AM}\), \(Z_{AM}\)không thay đổi, nên để \(U_{AM}\) đạt giá trị lớn nhất khi thay đổi C thì dòng điện Imax --> Xảy ra hiện tượng cộng hưởng: \(Z_L=Z_C\)
và \(I=\frac{U}{R+r}\)
Công suất của cuộn dây khi đó: \(P=I^2.r=\left(\frac{U}{R+r}\right)^2.r\) (*)
+ Nếu đặt vào 2 đầu AB một điện áp không đổi và nối tắt tụ C thì mạch chỉ gồm r nối tiếp với R (L không có tác dụng gì)
Cường độ dòng điện của mạch: \(I=\frac{25}{R+r}=0,5\Rightarrow R+r=50\)
Mà R = 40 suy ra r = 10.
Thay vào (*) ta đc \(P=\left(\frac{200}{50}\right)^2.10=160W\)
Bạn học đến điện xoay chiều rồi à. Học nhanh vậy, mình vẫn đang ở dao động cơ :(

Ta có điện áp hiệu dụng ở hai đầu đoạn mạch AM:
U A M = U R 2 + Z C 2 R 2 + Z L − Z C 2 = U 1 + Z L 2 − 2 Z L Z C R 2 + Z C 2
Để U A M không phụ thuộc vào R thì
Z L 2 − 2 Z L Z C R 2 + Z C 2 = 0 ⇒ Z L = 2 Z C
Chuẩn hóa R = 1.
→ Điện áp hiệu dụng cực đại giữa hai đầu cuộn dây
U L m a x = U R 2 + Z C 2 R = U 1 2 + 1 2 2 1 = 5 2 U
Đáp án D

Giải thích: Đáp án A
Điện áp hiệu dụng giữa hai đầu mạch MB: 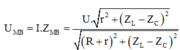
Chia cả tử và mẫu cho ![]() ta được:
ta được: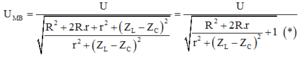
Để UMB cực tiểu thì mẫu của biểu thức (*) phải có giá trị cực đại:
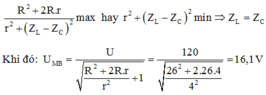
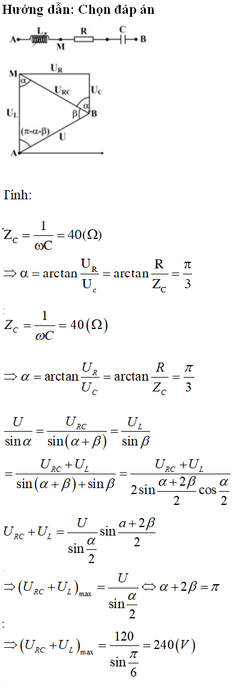

Đáp án B