Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
\(\lim\limits_{x\rightarrow-\infty}\dfrac{x+1}{\left(m^2+1\right)\sqrt{x^2-4}}=\lim\limits_{x\rightarrow-\infty}\dfrac{1+\dfrac{1}{x}}{-\left(m^2+1\right)\sqrt[]{1-\dfrac{4}{x^2}}}=-\dfrac{1}{m^2+1}\)
\(\lim\limits_{x\rightarrow+\infty}\dfrac{x+1}{\left(m^2+1\right)\sqrt{x^2-4}}=\dfrac{1}{m^2+1}\)
\(\Rightarrow\) ĐTHS có 2 tiệm cận ngang
\(\lim\limits_{x\rightarrow2^+}\dfrac{x+1}{\left(m^2+1\right)\sqrt{x^2-4}}=\dfrac{3}{0}=\infty\)
\(\lim\limits_{x\rightarrow-2^-}\dfrac{x+1}{\left(m^2+1\right)\sqrt{x^2-4}}=\dfrac{-1}{0}=\infty\)
\(\Rightarrow\) ĐTHS có 2 tiệm cận đứng
Vậy ĐTHS có 4 tiệm cận
tại sao nơi chỗ lim\(_{x->2^+}\) và limx->-2- ở dưới mẫu lại bằng 0 vậy ạ?
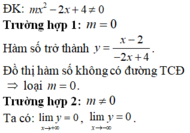
Suy ra đồ thị hàm số có 1 đường TCN y = 0.
Do đó đồ thị hàm số có đúng 2 đường tiệm cận đồ thị hàm số có đứng 1 đường tiệm cận đứng phương trình m x 2 - 2 x + 4 = 0 có nghiệm kép hoặc có 2 nghiệm phân biệt trong đó có 1 nghiệm x = 2.
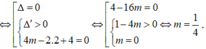
Vậy có 1 giá trị của m thỏa mãn yêu cầu bài toán.
Chọn A
Chọn đáp án A.
⇒ y = 1 ; y = 3 là các đường tiệm cận ngang và
Đáp án là C
Hàm số đã cho có tập xác định
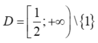
Ta có 
nên đồ thị nhận đường thẳng 
làm tiệm cận ngang.
nên đồ thị nhận đường thẳng x = 1 làm tiệm cận đứng.
Vậy đồ thị hàm số đã cho có 2 đường tiệm cận đứng và ngang.
Chọn B
Ta có:
.
.
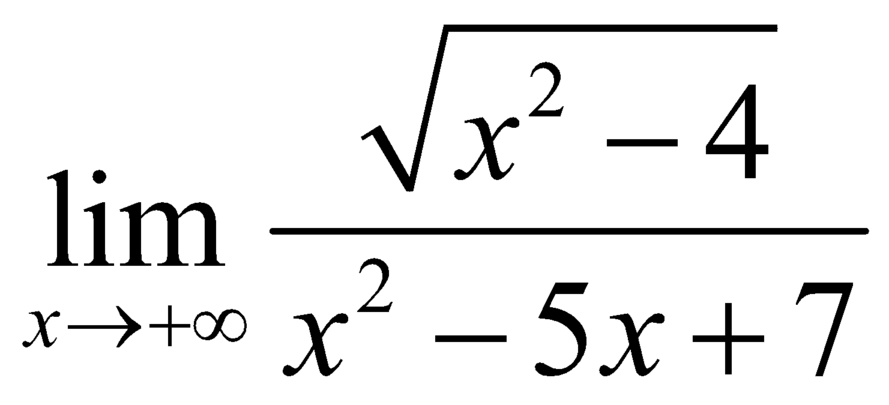
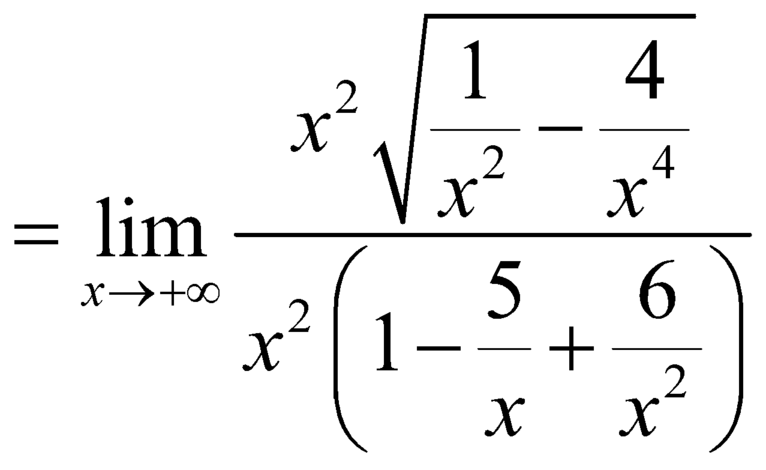
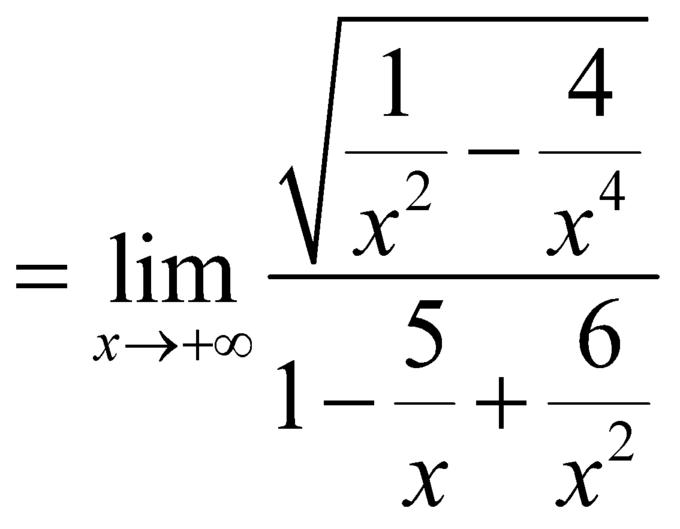
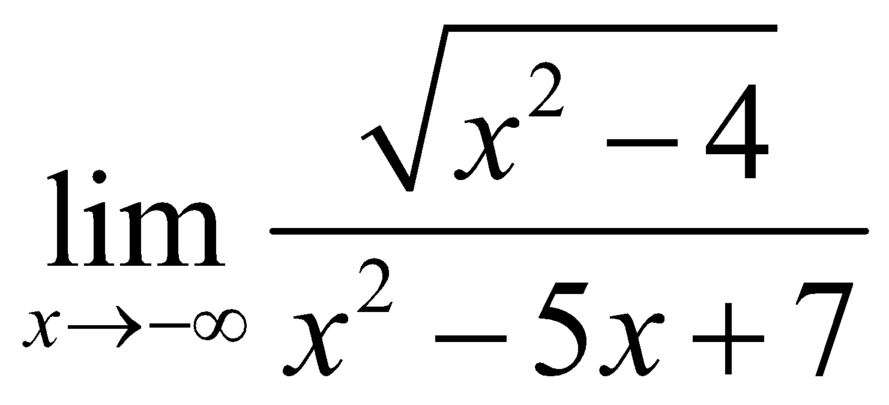
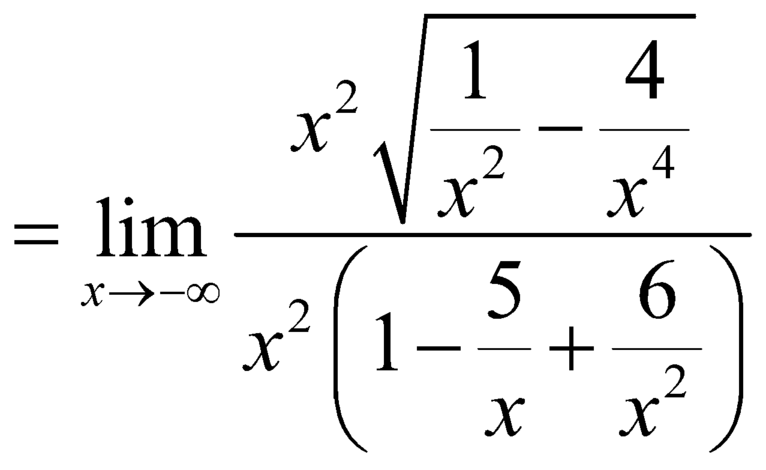
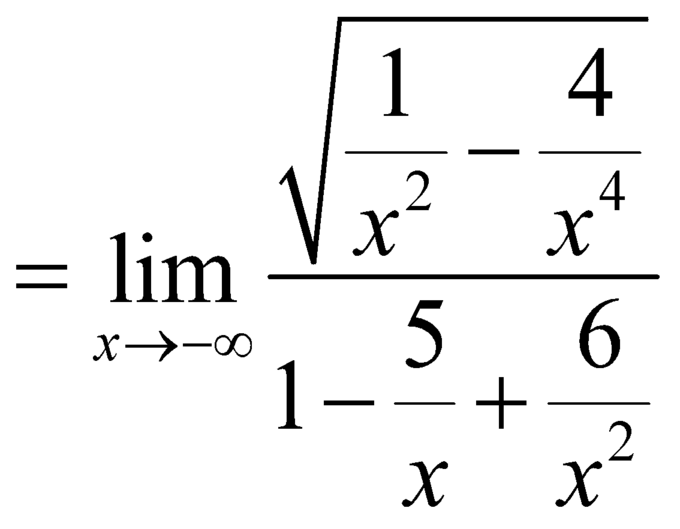
Nên đồ thị hàm số có đường tiệm cận ngang là 
.
Xét 
.
.
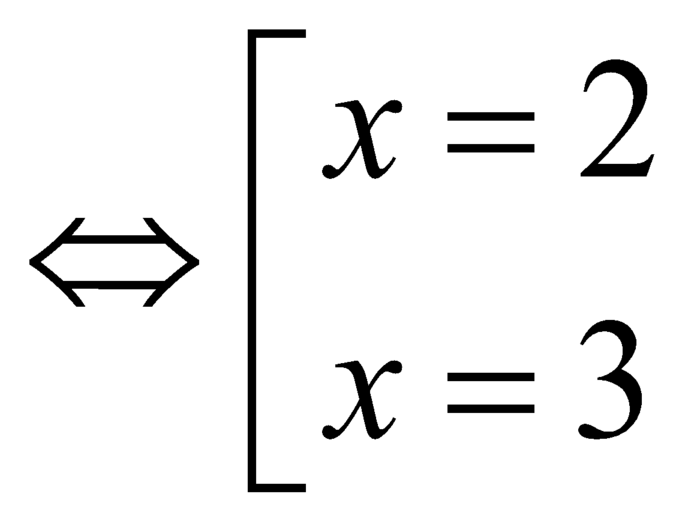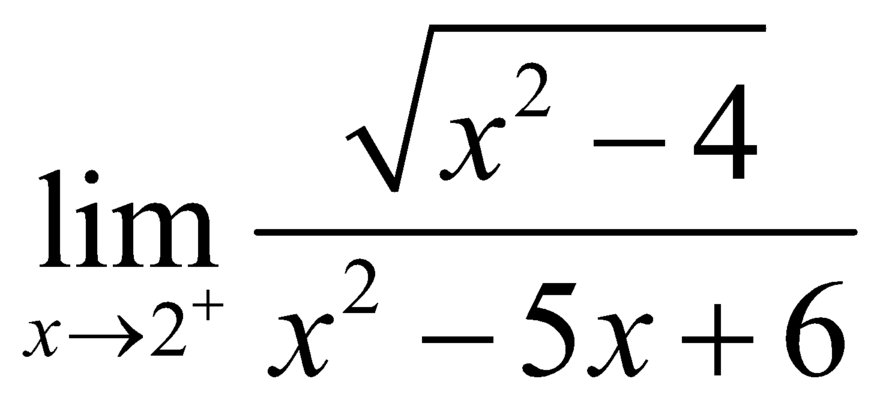
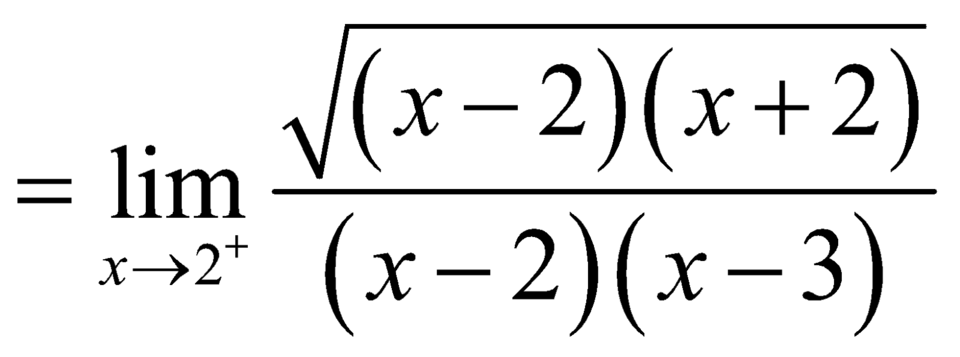
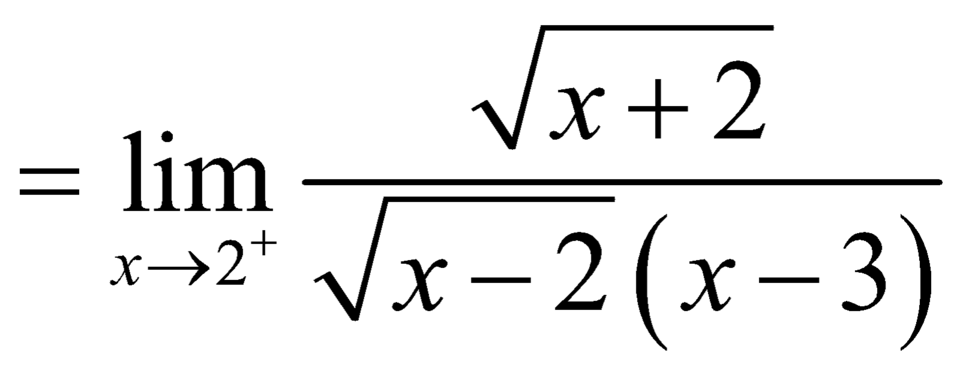
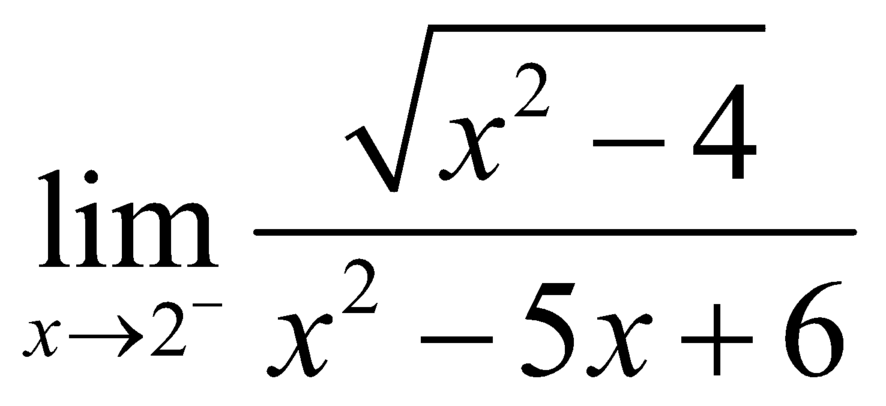không tồn tại.
Nên đồ thị hàm số có đường tiệm cận đứng là 
.
.
.
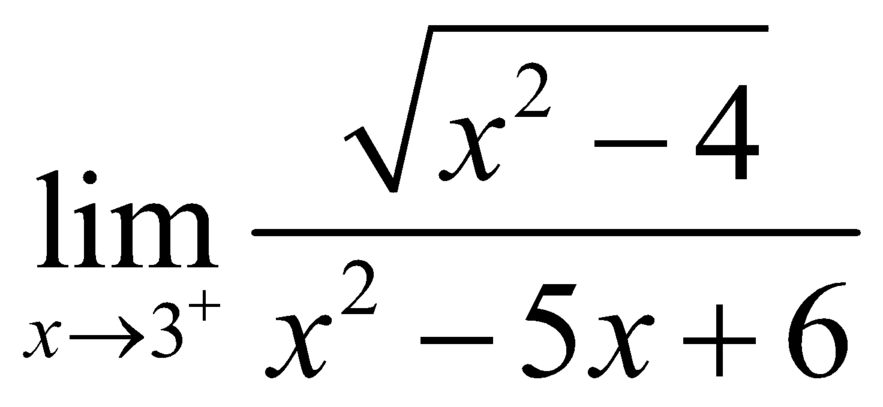
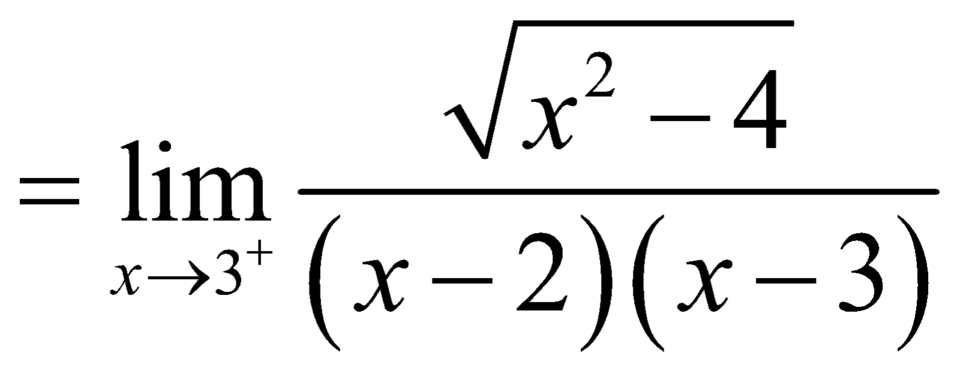
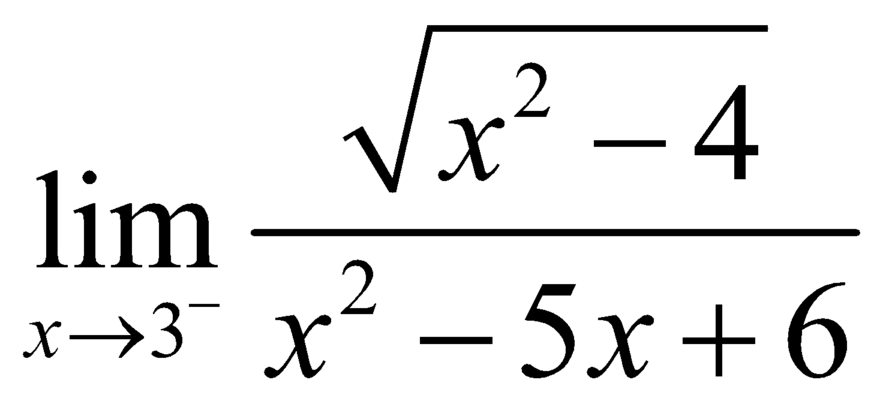
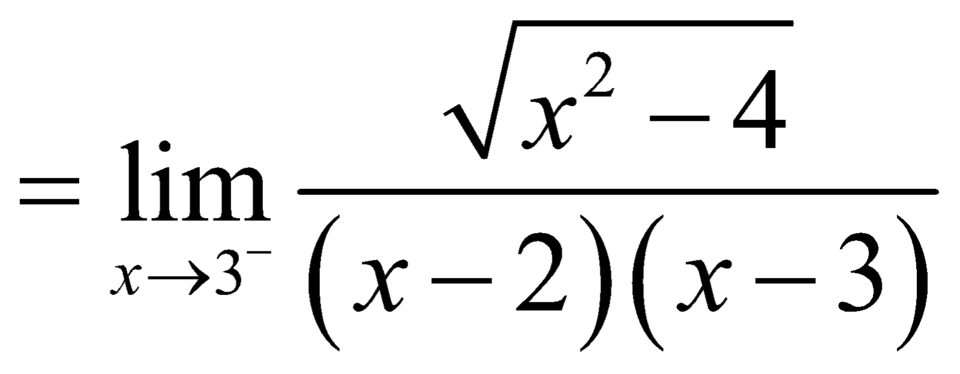
Nên đồ thị hàm số có đường tiệm cận đứng là 
.
Vậy đồ thị hàm số có 3 đường tiệm cận đứng và tiệm cận ngang.
Chọn C.
Hàm số có tập xác định là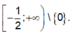 
Ta có
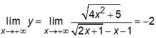
=> y = -2 là đường tiệm cận ngang của đồ thị hàm số đã cho.
Mặt khác,
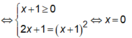
Với mọi x > 0 ta có 
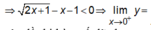
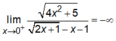
=> x = 0 là đường tiệm cận đứng của đồ thị hàm số đã cho.
Vậy hàm số đã cho có 2 đường tiệm cận.
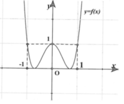
Chọn D
Phương pháp
Nếu
thì y =
y
0
là phương trình đường tiệm cận ngang của đồ thị hàm số.
Nếu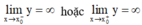
thì x =
x
0
là phương trình đường tiệm cận ngang của đồ thị hàm số.
Cách giải:
TXĐ: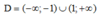
Ta có: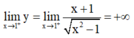
nên x = 1 là tiệm cận đứng của đồ thị hàm số.
nên x = -1 không là tiệm cận đứng của đồ thị hàm số.
Ta có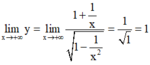
=> tiệm cận ngang y = 1
Lại có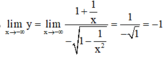
=> tiệm cận ngang y = -1
Đồ thị hàm số y = x + 1 x 2 - 1 có tất cả 3 tiệm cận đứng và tiệm cận ngang.