K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
AH
Akai Haruma
Giáo viên
5 tháng 10 2021
Lời giải:
Nói đơn giản thế này. Khi đề cho: Cho đồ thị hàm số $y=x+2$
- Hàm số: chính là $y=x+2$, biểu diễn mối quan hệ giữa biến $x$ và biến $y$. Hàm số hiểu đơn giản giống như phép biểu diễn mối quan hệ giữa hai biến.
- Đồ thị hàm số (hay đồ thị): Khi có hàm số rồi, người ta muốn biểu diễn nó trên mặt phẳng tọa độ ra được 1 hình thù nào đó thì đó là đồ thị hàm số. Ví dụ, đths $y=x+2$ có dạng như thế này:
AH
Akai Haruma
Giáo viên
5 tháng 10 2021
- Tọa độ giao điểm của hai đồ thị: Khi ta vẽ được đồ thị trên mặt phẳng tọa độ, 2 đồ thị đó giao nhau ở vị trí nào thì đó chính là tọa độ giao điểm. Ví dụ, trên mp tọa độ ta có 2 đồ thị $y=-2x+3$ và $y=x+6$ chả hạn. Điểm $A$, có tọa độ $(-1,5)$ chính là giao điểm. Như vậy, $(-1,5)$ là tọa độ giao điểm.
- Nhìn hình vẽ của đồ thị chỉ giúp ta có cái nhìn trực quan hơn. Khi muốn tìm giao điểm của 2 đồ thị hàm số, người ta thường dùng hàm số để tìm cho nhanh, vì hàm số biểu diễn mối quan hệ giữa hai biến một cách "số hóa" hơn.
- Với nhiều hàm số trở lên thì ta cứ xét từng cặp 1 thôi.
MT
12 tháng 7 2021
Đề ví dụTimf x không âm biết căn (x-1)=...... Đề bải x không âm thì chỉ cần x>=0 thôi chứ ạ. Chỉ rõ chio mình hiểu nhá
12 tháng 7 2021
Vì khi lấy ĐKXĐ thì lấy cả biểu thức trong căn mới đúng
12 tháng 7 2021
Thì ĐKXĐ là phải lấy tất cả các biểu thức trong căn phải không âm
AH
Akai Haruma
Giáo viên
12 tháng 7 2021
Bạn nhớ rằng $\sqrt{a}$ xác định khi mà $a\geq 0$, hay $a$ không âm.
Cho $a=x-1$ thì để $\sqrt{x-1}$ xác định thì $x-1\geq 0$
$\Leftrightarrow x\geq 1$
DT
2
LN
30 tháng 10 2017
cô này troll học sinh rồi
dễ thế này cx ko làm đc bó tay chấm com
CM
22 tháng 10 2017
Vẽ hình:
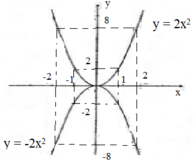
a) Nếu a > 0 thì hàm số đồng biến khi x > 0, nghịch biến khi x < 0
Với x = 0 thì hàm số đạt giá trị nhỏ nhất bằng 0. Không có giá trị nào của hàm số để đạt giá trị lớn nhất.
Nếu a < 0 thì hàm số đồng biến khi x < 0, nghịch biến khi x > 0.
Hàm số đạt giá trị lớn nhất y = 0 khi x = 0 . Không có giá trị bào của x để hàm số đạt giá trị nhỏ nhất.
b) Đồ thị hàm số y = a x 2 là đường cong (đặt tên là parabol) đi qua gốc tọa độ nhận trục tung Oy làm trục đối xứng.
Nếu a > 0 thì đồ thị nằm trên trục hoành, điểm O là điểm thấp nhất đồ thị (gọi là đỉnh parabol).
Nếu a < 0 thì đồ thị nằm bên dưới trục hoành, điểm O là điểm cao nhất của đồ thị.
CM
28 tháng 6 2017
Vẽ hình:
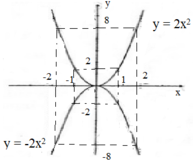
Nếu a > 0 thì hàm số đồng biến khi x > 0, nghịch biến khi x < 0
Với x = 0 thì hàm số đạt giá trị nhỏ nhất bằng 0. Không có giá trị nào của hàm số để đạt giá trị lớn nhất.
Nếu a < 0 thì hàm số đồng biến khi x < 0, nghịch biến khi x > 0.
Hàm số đạt giá trị lớn nhất y = 0 khi x = 0 . Không có giá trị bào của x để hàm số đạt giá trị nhỏ nhất.
CM
13 tháng 3 2018
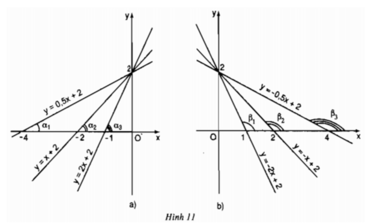
Ta có: β1 < β2 < β3 và các giá trị tương ứng của hệ số a trong các hàm số
-2 < -1 < -0,5
Nhận xét : Khi hệ số a âm (a < 0) thì góc tạo bởi đường thẳng y = ax + b và trục Ox là góc tù, hệ số a càng lớn thì góc càng lớn nhưng vẫn nhỏ hơn 180o
23 tháng 11 2023
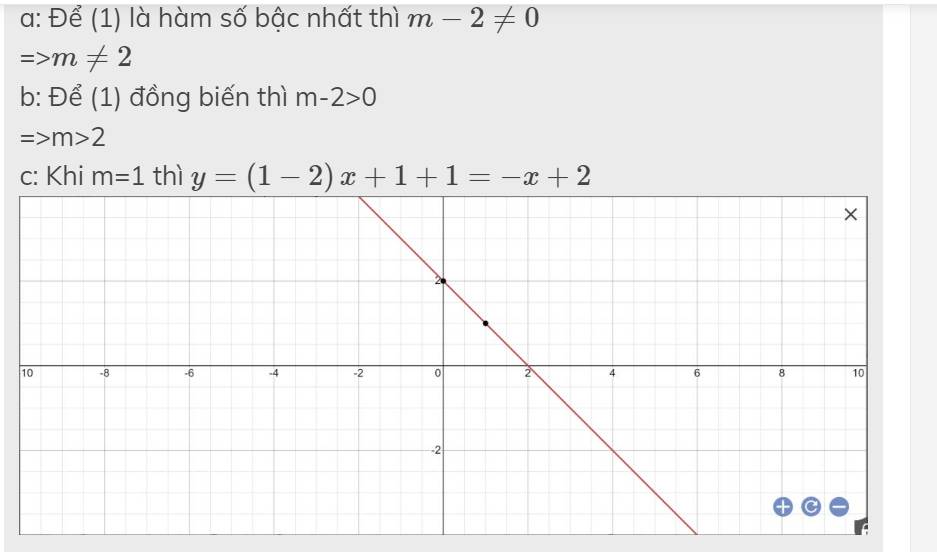
h: Khi m=3 thì \(y=\left(3-2\right)x+3+1=x+4\)
Gọi \(\alpha\) là góc tạo bởi đồ thị hàm số y=x+4 với trục Ox
\(tan\alpha=a=1\)
=>\(\alpha=45^0\)
y=x+4
=>x-y+4=0
Khoảng cách từ O(0;0) đến đường thẳng x-y+4=0 là:
\(\dfrac{\left|0\cdot1+0\cdot\left(-1\right)+4\right|}{\sqrt{1^2+\left(-1\right)^2}}=\dfrac{4}{\sqrt{2}}=2\sqrt{2}\)
Đồ thị hàm số $x=0$ là đồ thị được biểu diễn bởi tập hợp các điểm có hoành độ bằng 0 và tung độ bất kỳ.
Hay chính là trục tung.
Chị ơi