Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.
Để ý khi x = 0 thì y = 2 nên loại cả ba phương án B, C và D.

Chọn D
Ta có

Vì f'(x) luôn đồng biến trên
ℝ
nên ![]() , do đó: a > 0 và b > 0
, do đó: a > 0 và b > 0
Mặt khác vì đồ thị hàm số không cắt trục Ox nên chọn đáp án D.

Chọn B.
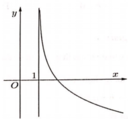
Nhận xét hàm số đã cho là hàm nghịch biến( loại A và C).
Mặt khác đồ thị hàm số đã cho nhận x = 1 là đường tiệm cận đứng
(Đáp án D là có tiệm cận ngang; không có tiệm cận đứng)

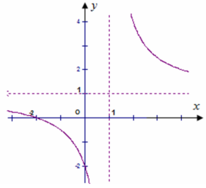
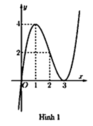
Dựa vào đồ thị hình vẽ ta thấy:
+ Hàm số đã cho phải là hàm số đồng biến trên tập xác định của nó là
( loại C và D)
Hàm số đã cho nhận trục Oy là đường tiệm cận ngang
Chọn B.

Đáp án C.
Đồ thị có:
+) Tiệm cận đứng: x = 1. Tiệm cận ngang: y = 1 => loại B, D.
+) Giao với trục hoành tại điểm A(-2;0) => loại A;
+) Vậy Đáp án C.
+) Mặt khác đồ thị nằm cung phần tư thứ I, III nên y’ < 0

Chọn A
Cách 1:
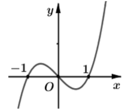
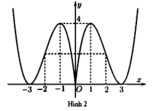
+) Ta thấy Hình 2 có được là do ta giữ nguyên phần đồ thị của hàm số x 3 - 6 x 2 + 9 x thuộc trục Oy và nằm bên phải của trục Oy và sau đó lấy đối xứng phần đồ thị này qua Oy. Do đó ta suy ra Hình 2 là đồ thị của hàm số x 3 - 6 x 2 + 9 x .
Ghi nhớ: Từ đồ thị hàm số y = f(x), muốn vẽ đồ thì của hàm số y = f x thì ta làm như sau:
Bước 1: Giữ nguyên phần đồ thị hàm số y = f(x) thuộc trục Oy (nếu có) và nằm bên phải trục Oy
Bước 2: Ta lấy đối xứng phần đồ thị đó qua trục Oy.
Cách 2:
Từ hình 2 ta thấy đồ thị nhận trục tung làm trục đối xứng nên suy ra đây là đồ thị của hàm số chẵn, do đó ta loại được phương án C và D. Lại thấy đồ thị đi qua gốc tọa độ nên suy ra ta loại phương án B. Vậy đáp án là A.
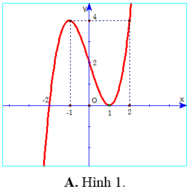
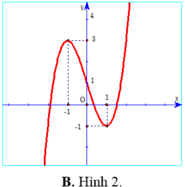
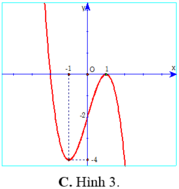
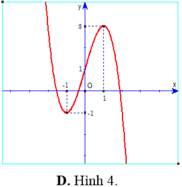
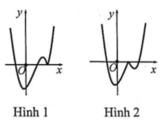
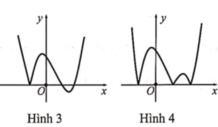
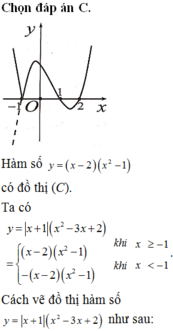

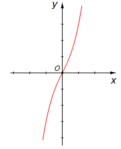
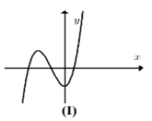
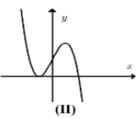
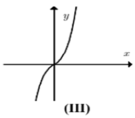

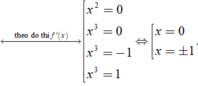
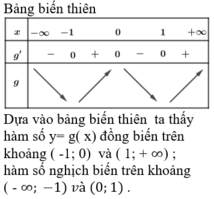
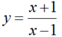
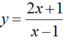
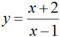
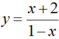
Chọn C
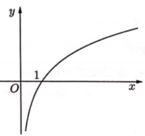
Dựa vào đồ thị hình vẽ ta thấy:
Hàm số đã cho phải là hàm số đồng biến trên tập xác định của nó là R.(loại A và B)
Hàm số đã cho nhận trục Ox là đường tiệm cận ngang ( loại D ).