

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




Đáp án C
+ Ta có phương trình độc lập thời gian giữa v và x là elip có dạng: x 2 A 2 + v 2 ( ω A ) 2 = 1
+ Gọi chiều dài 1 ô là n, theo định nghĩa elip, ta có:
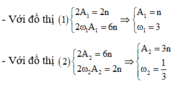
+ Theo đề bài: Lực kéo về cực đại tác dụng lên hai vật trong quá trình dao động là bằng nhau nên:
k 1 A 1 = k 2 A 2 ⇔ m 1 ω 1 2 A 1 = m 2 ω 2 2 A 2
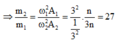

Đáp án là C
Cực kéo về cực đại tác dụng lên hai vật trong quá trình dao động là bằng nhau.
ð F=k|x|=> Fmax=k.A=mw2A
ð m1ω21A1=m2ω22A2=>m1m2=ω21.A1ω22.A2
ð 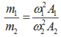
Theo đồ thị:
+ Độ dài trục lớn elip = 2a
+ Độ dài trục bé elip =2b
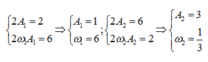

+ Nhìn vào đồ thị ta thấy: A 2 = 3 A 1 ⇒ A 2 = v 1 max = A 1 ω 1 A 1 = v 2 max = A 2 ω 2 ⇒ ω 1 ω 2 = A 2 2 A 1 2 1
+ Theo giải thiết: k 1 A 1 = k 2 A 2 ⇒ m 1 ω 1 2 A 1 = m 2 ω 2 2 A 2 ⇒ m 2 m 1 = ω 1 2 ω 2 2 A 1 A 2 2
→ Từ (1) và (2) m 2 m 1 = A 1 A 2 2 = 27
Chọn đáp án C

Đáp án C
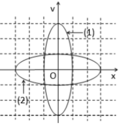
Quy ước rằng 1 đơn vị trục hoành ứng với n, 1 đơn vị trục tung ứng với n’. Từ đồ thị ta thấy:
+ Vật (1): A 1 = n v 1 max = A 1 ω 1 = 3 n ' ⇒ ω 1 = 3 n ' n
+ Vật (2): A 2 = 3 n v 2 max = A 2 ω 2 = n ' ⇒ ω 2 = n ' 3 n
Có F k v 1 max = F k v 2 max ⇒ k 1 A 1 = k 2 A 2 ⇒ m 1 ω 1 2 A 1 = m 2 ω 2 2 A 2
⇒ m 2 m 1 = ω 1 2 A 1 ω 2 2 A 2 = 9 n ' 2 n 2 . n n ' 2 9 n 2 .3 n = 27

Đáp án C
Từ đồ thị, ta nhận thấy

Từ (2) và (1) suy ra
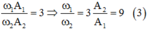
Hai dao động có cùng độ lớn lực kéo về cực đại nên 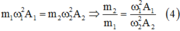
Từ (3) và (4) ta tìm được m 2 m 1 = 27

Đồ thị biểu diễn mối liên hệ giữa li độ x và vận tốc v của vật dao động điều hòa là một elip.
Đáp án D

+ Từ đồ thị dễ thấy pha ban đầu của 3 đồ thị lần lượt là
φ 1 = π 2 (do t = 0 đang ở vtcb về biên âm)
φ 1 = π (do t = 0 đang ở vt biên âm)
φ 3 = − π 2 (do t = 0 đang ở vtcb về biên dương)
+ Kết hợp a nhanh pha hơn v góc π/2, v lại nhanh pha hơn x góc π/2, a và x ngược pha nên suy ra
Đường (1), (2), (3) lần lượt biểu diễn x, v, a.
Chọn đáp án C

Động năng: \(W_đ=\frac{1}{2}k.x^2\)
Như vậy động năng tỉ lệ với li độ theo hàm bậc 2, do đó đồ thị biểu diễn sự phụ thuộc của động năng theo li độ là parabol.
Đáp án B.

Từ công thức độc lập, ta có: \(A^2 = x^2+\frac{v^2}{\omega ^2} \Rightarrow (\frac{x}{A})^2+(\frac{v}{\omega A})^2=1\), đây là phương trình của đường Elip.