Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
ln 100 = ln 2 2 .5 2 = 2 ln 2 + 2 ln 5
= 2 ln 2 + ln 5 = 2 a + ln 2. l o g 2 5
= 2 a + ln 2. 1 l o g 5 2 = 2 a + a . 1 b 2 = 2 a b + 4 a b .

Đáp án là D.
+ G x = 3 4 x 2 − 1 40 x 3 ⇒ G ' x = 3 2 x − 3 40 x 2 = 0 ⇔ x = 0 x = 20
+ Vì x>0 nên x = 20mg.

Đáp án A.
Ta có G ' x = 0 , 024 x 2 30 - x = 1 , 44 x - 0 , 072 x 2 ⇒ G ' x = 0 ⇔ 1 , 44 x - 0 , 072 x 2 = 0
⇔ [ x = 0 x = 20
Suy ra G 0 = 0 G 20 = 96 ⇒ M a x G ( x ) = G ( 20 ) = 96 .

Xét hàm số C t = 0 , 28 t t 2 + 4 liên tục trên khoảng 0 ; 24 . Áp dụng bất đẳng thức Cauchy ta có C t = 0 , 28 t t 2 + 4 ≤ 0 , 28 t 2 t 2 . 4 = 7 100
Dấu “=” xảy ra t 2 = 4 ⇔ t = 2
Vậy sau 2 giờ nồng độ thuốc hấp thu trong máu là cao nhất.
Đáp án C

Đáp án D
Phương pháp giải: Công thức tính diện tích hình phẳng giới hạn bởi hai đồ thị hàm số
Lời giải:
Diện tích S của hình phẳng D được tính theo công thức là S = ∫ a b f x − g x d x

Đáp án C
Phương pháp: Dựa vào công thức ứng dụng tích phân để tính thể tích vật tròn xoay.
Cách giải: V =
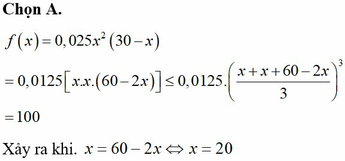

Đáp án B
G ( x ) = 0 , 035 x 2 ( 15 − x )
Bệnh nhân giảm huyết áp nhiều nhất khi và chỉ khi G(x) đạt giá trị lớn nhất
G ' ( x ) = 0 , 105 x 2 + 1 , 05 x
Cho G ' ( x ) = 0 ⇔ x = 0 x = 10
G(x) max khi và chỉ khi x = 10