Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giả sử bốn điểm A, B, C, D tạo thành một hình bình hành ta có:
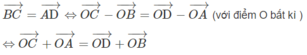
Ngược lại, giả sử ta có hệ thức:
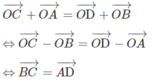
Vì A, B, C, D không thẳng hàng nên tứ giác ABCD là hình bình hành.

+) Trước hết, điều kiện cần và đủ để tứ giác ABCD là hình bình hành là: 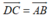 .
.
+) Với mọi điểm O bất kì khác A, B, C, D ta có:
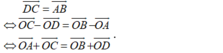
- Vậy điều kiện cần và đủ để tứ giác ABCD là hình bình hành là:
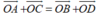

Chọn B.
- Trước hết, điều kiện cần và đủ để tứ giác ABCD là hình bình hành là:
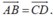
- Với mọi điểm O bất kì khác A, B, C, D ta có:
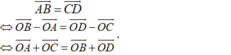

Ta có
(1) Điều kiện cần và đủ để C là trung điểm của đoạn AB là B A → = - 2 A C →
(3) Điều kiện cần và đủ để M là trung điểm của đoạn PQ là P Q → = 2 P M →
Phát biểu sai: (2) Điều kiện cần và đủ để C là trung điểm của đoạn AB là
Do đó câu (1) và câu (3) là đúng.
Chọn A.

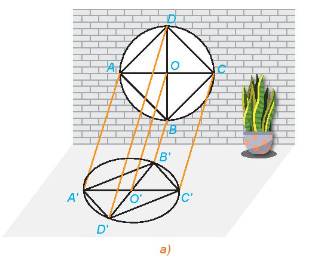
a) Hình chiếu O’ của điểm O nằm trên đoạn A’C’.
b) Hình chiếu song song của AB và CD song song với AB và CD.
c) Hình chiếu O’ của điểm O là trung điểm của đoạn A’C’.

Điểm O là trung điểm của đoạn AB khi và chỉ khi OA= OB và là ngược hướng.Vậy
O A → + O B → = 0 →