Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a:
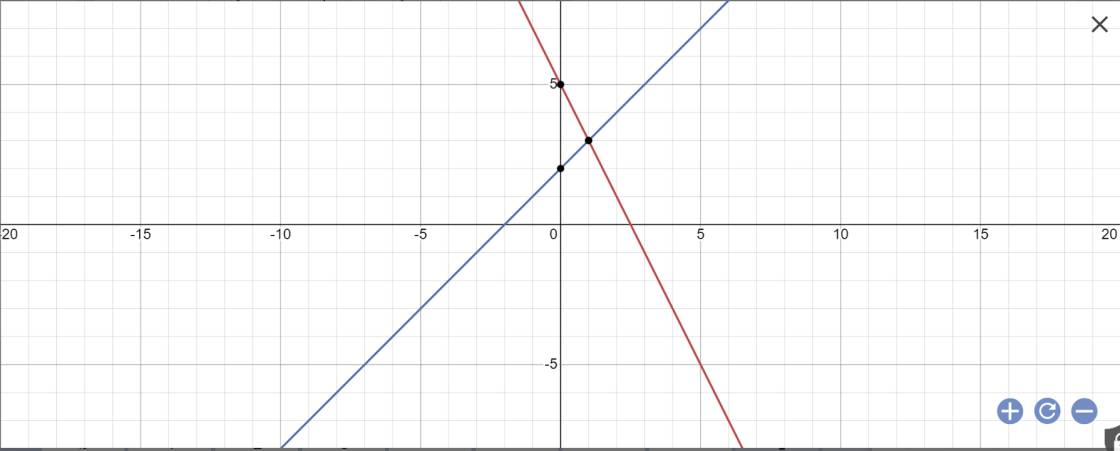
b: Phương trình hoành độ giao điểm là:
-2x+5=x+2
=>-2x-x=2-5
=>-3x=-3
=>x=1
Thay x=1 vào y=x+2, ta được;
y=1+2=3
Vậy: A(1;3)
c: Sửa đề: Tính góc tạo bởi đường thẳng y=x+2 với trục Ox
Gọi \(\alpha\) là góc tạo bởi đường thẳng y=x+2 với trục Ox
y=x+2 nên a=1
=>\(tan\alpha=a=1\)
=>\(\alpha=45^0\)
d: Vì (d)//y=-3x-1 nên \(\left\{{}\begin{matrix}a=-3\\b\ne-1\end{matrix}\right.\)
Vậy: (d): y=-3x+b
Thay x=1 và y=3 vào (d), ta được:
\(b-3\cdot1=3\)
=>b-3=3
=>b=6(nhận)
Vậy: (d): y=-3x+6

Cho x= 0 thì y = 1 ta được điểm (0 ;1)
Cho y = 0 thì x = 1 3 ta được điểm 1 3 ; 0
Vậy tọa độ các giao điểm của đồ thị hàm số y = - 3 x + 1 với các trục Ox, Oy lần lượt là: 1 3 ; 0 và (0;1)

a: Vì (d) đi qua A(3;-4) và (0;2) nên ta có hệ phương trình:
\(\left\{{}\begin{matrix}3a+b=-4\\b=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-2\\b=2\end{matrix}\right.\)
b: vì (d)//y=-4x+4 nên a=-4
Vậy:(d): y=-4x+b
Thay x=-2 và y=0 vào (d), ta được:
b+8=0
hay b=-8

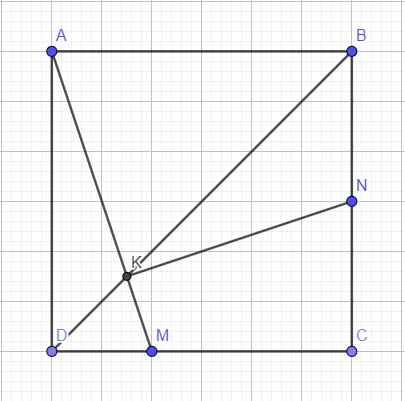
Talet: \(\dfrac{KM}{AK}=\dfrac{DM}{AB}=\dfrac{1}{3}\Rightarrow KM=\dfrac{1}{3}AK\Rightarrow KM=\dfrac{1}{4}AM\Rightarrow\overrightarrow{KM}=\dfrac{1}{4}\overrightarrow{AM}\)
Mà \(\overrightarrow{AM}=\overrightarrow{AD}+\overrightarrow{DM}=\overrightarrow{AD}+\dfrac{1}{3}\overrightarrow{AB}\Rightarrow\overrightarrow{KM}=\dfrac{1}{4}\overrightarrow{AD}+\dfrac{1}{12}\overrightarrow{AB}\)
\(\overrightarrow{KN}=\overrightarrow{KM}+\overrightarrow{MC}+\overrightarrow{CN}=\dfrac{1}{4}\overrightarrow{AD}+\dfrac{1}{12}\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{AB}-\dfrac{1}{2}\overrightarrow{AD}\)
\(=\dfrac{3}{4}\overrightarrow{AB}-\dfrac{1}{4}\overrightarrow{AD}\)
\(\Rightarrow\overrightarrow{AM}.\overrightarrow{KN}=\left(\overrightarrow{AD}+\dfrac{1}{3}\overrightarrow{AB}\right)\left(\dfrac{3}{4}\overrightarrow{AB}-\dfrac{1}{4}\overrightarrow{AD}\right)=\dfrac{1}{4}AB^2-\dfrac{1}{4}AD^2=0\)
\(\Rightarrow AM\perp KN\Rightarrow\) đường thẳng KN nhận (10;1) là 1 vtpt
Phương trình NK:
\(10\left(x-0\right)+1\left(y-2019\right)=0\Leftrightarrow10x+y-2019=0\)
\(d\left(O;NK\right)=\dfrac{\left|-2019\right|}{\sqrt{10^2+1^2}}=\dfrac{2019}{\sqrt{101}}\)

a) Vì P là hình chiếu vuông góc của M trên Ox nên điểm P biểu diễn hoành độ của điểm M là số \({x_o}\)
Ta có: vectơ \(\overrightarrow {OP} \) cùng phương, cùng hướng với \(\overrightarrow i \) và \(\left| {\overrightarrow {OP} } \right| = {x_o} = {x_o}.\left| {\overrightarrow i } \right|\)
\( \Rightarrow \overrightarrow {OP} = {x_o}.\;\overrightarrow i \).
b) Vì Q là hình chiếu vuông góc của M trên Oy nên điểm Q biểu diễn tung độ của điểm M là số \({y_o}\)
Ta có: vectơ \(\overrightarrow {OQ} \) cùng phương, cùng hướng với \(\overrightarrow j \) và \(\left| {\overrightarrow {OQ} } \right| = {y_o} = {y_o}.\left| {\overrightarrow j } \right|\)
\( \Rightarrow \overrightarrow {OQ} = {y_o}.\;\overrightarrow j \).
c) Ta có: \(\overrightarrow {OM} = OM\).
Mà \(O{M^2} = O{P^2} + M{P^2} = O{P^2} + O{Q^2} = {x_o}^2 + {y_o}^2\)
\( \Rightarrow \left| {\overrightarrow {OM} } \right| = \sqrt {{x_o}^2 + {y_o}^2} \)
d) Ta có: Tứ giác OPMQ là hình chữ nhật, cũng là hình bình hành nên \(\overrightarrow {OM} = \overrightarrow {OP} + \overrightarrow {OQ} \)
\( \Rightarrow \overrightarrow {OM} = {x_o}.\;\overrightarrow i + {y_o}.\;\overrightarrow j \)