Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 3:
Phương trình hoành độ giao điểm:
\(x^3=x^2-4x+4\Leftrightarrow x^3-x^2+4x-4=0\Rightarrow x=1\)
\(x^3=0\Rightarrow x=0\)
\(x^2-4x+4=0\Rightarrow x=2\)
Diện tích hình phẳng:
\(S=\int\limits^1_0x^3dx+\int\limits^2_1\left(x^2-4x+4\right)dx=\frac{7}{12}\)
Câu 4:
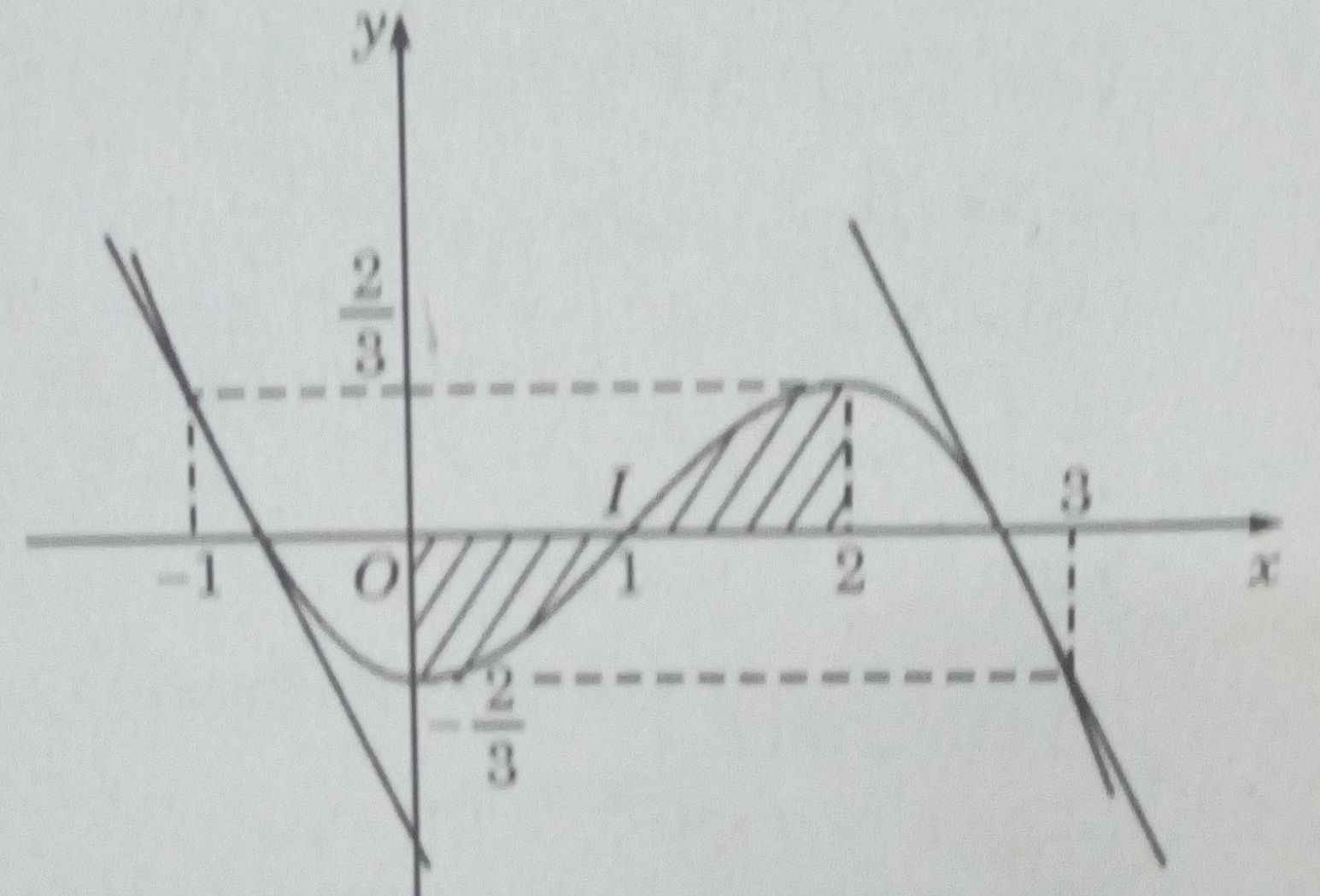
Phương trình hoành độ giao điểm:
\(x^3-3x+2=x+2\Leftrightarrow x^3-4x=0\Rightarrow\left[{}\begin{matrix}x=-2\\x=0\\x=2\end{matrix}\right.\)
Diện tích hình phẳng:
\(S=\int\limits^0_{-2}\left(x^3-3x+2-x-2\right)dx+\int\limits^2_0\left(x+2-x^3+3x-2\right)dx=8\)
Câu 1:
Phương trình hoành độ giao điểm: \(cosx=0\Rightarrow x=\frac{\pi}{2}\)
\(\Rightarrow S=\int\limits^{\frac{\pi}{2}}_0cosxdx-\int\limits^{\pi}_{\frac{\pi}{2}}cosxdx=2\)
Câu 2:
Phương trình hoành độ giao điểm: \(x.e^x=0\Rightarrow x=0\)
\(\Rightarrow S=\int\limits^3_0xe^x-\int\limits^0_{-2}xe^xdx\)
Xét \(I=\int x.e^xdx\Rightarrow\left\{{}\begin{matrix}u=x\\dv=e^xdx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=dx\\v=e^x\end{matrix}\right.\)
\(\Rightarrow I=x.e^x-\int e^xdx=xe^x-e^x+C=\left(x-1\right)e^x+C\)
\(\Rightarrow S=\left(x-1\right)e^x|^3_0-\left(x-1\right)e^x|^0_{-2}=2e^3+1-\left[-1+\frac{3}{e^2}\right]=2e^3+2-\frac{3}{e^2}\)

a) Diện tích hình phẳng cần tìm là:
S=2∫−1(x2+1)dx=(x33+x)∣∣2−1=6
b) Diện tích hình phẳng cần tìm là:
S=e∫1e| lnx |dx=e∫1e|lnx|dx+e∫1|lnx|dx=−1∫1elnxdx+e∫1lnxdxS=∫1ee|lnx|dx=∫1ee|lnx|dx+∫1e|lnx|dx=−∫1e1lnxdx+∫1elnxdx
Mặt khác:
∫lnxdx=xlnx−∫xdlnx=xlnx−∫dx=xlnx−x+C∫lnxdx=xlnx−∫xdlnx=xlnx−∫dx=xlnx−x+C
Do đó:
S=−1∫1elnxdx+e∫1lnxdx=1e∫1lnxdx+e∫1xdx=(xlnx−x)∣∣∣1e1+(xlnx−x)∣∣e1=2(1- \(\dfrac{1}{e}\))
Khó quá, làm mà điên não

a) Khi a = 0 ta có hàm số: y=−13x3−x2+3x−4y=−13x3−x2+3x−4
- Tập xác định : (-∞, +∞)
- Sự biến thiên: y’= -x2 – 2x + 3
y’=0 ⇔ x = 1, x = -3
Trên các khoảng (-∞, -3) và (1, +∞), y’ < 0 nên hàm số nghịch biến.
Trên khoảng (-3, 1), y’ > 0
_ Cực trị:
Hàm số đạt cực đại tại x = 1, yCD=−73yCD=−73
Hàm số đạt cực tiểu tại x = -3, yCT=−13yCT=−13
_ giới hạn vô cực : limx→+∞=−∞,limx→−∞=+∞limx→+∞=−∞,limx→−∞=+∞
Bảng biến thiên:
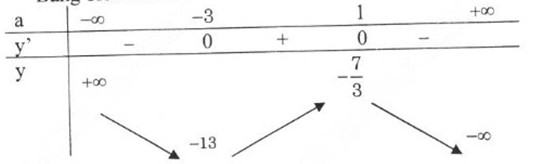
Đồ thị hàm số:
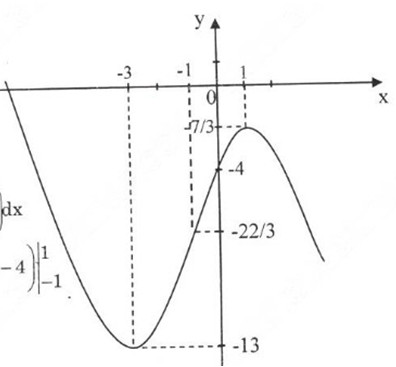
Đồ thị cắt trục tung tại y = -4
Đồ thị cắt trục hoành tại x ≈ 5, 18
b) Hàm số y=−13x3−x2+3x−4y=−13x3−x2+3x−4 đồng biến trên khoảng (-3, 1) nên:
y < y(1) = −73−73 < 0, ∀x ∈ (-1, 1)
Do đó , diện tích cần tính là:
∫1−1(−13x3−x2+3x−4)dx=263
Xem thêm tại: http://loigiaihay.com/cau-2-trang-145-sgk-giai-tich-12-c47a26419.html#ixzz4czxQ4IGx

Tập xác định : \(D=R\backslash\left\{1\right\}\)
\(M\in Ox\Rightarrow M\left(x_0;0\right)\) đường thẳng qua M với hệ số góc k có phương trình \(y=k\left(x-x_0\right)\) \(\left(\Delta\right)\)
\(\left(\Delta\right)\) là tiếp tuyến của đồ thì khi hệ \(\begin{cases}\frac{x^2}{x-1}=k\left(x-x_0\right)\\\frac{x^2-2x}{\left(x-1\right)^2}=k\end{cases}\) có nghiệm
\(\Rightarrow\frac{x^2}{x-1}=\frac{x^2-2x}{\left(x-1\right)^2}\left(x-x_0\right)\Leftrightarrow x\left[\left(x_0+1\right)x-2x_0\right]=0\)
\(\Rightarrow\left[\begin{array}{nghiempt}x=0\\x=\frac{2x_0}{x_0+1}\end{array}\right.\) với \(x_0\ne-1\)
* Với \(x_0=0\Rightarrow k=0\)


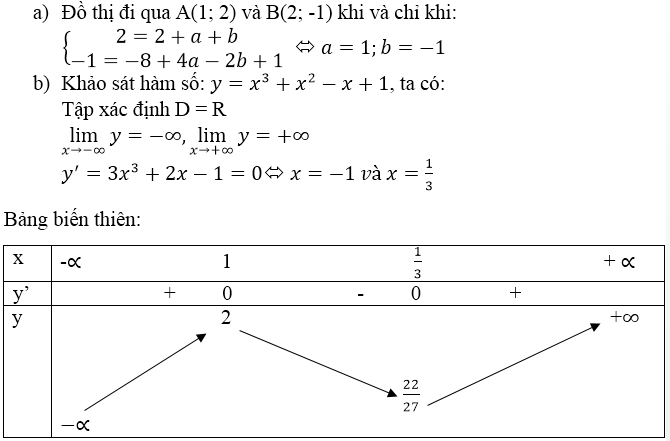
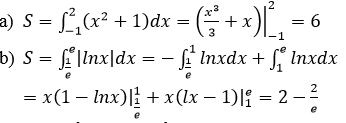

Ta có x 3 ≥ 0 trên đoạn [1 ; 8] nên
Chọn B