Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án A
+ Hiệu suất truyền tải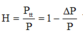 
với P là công suất truyền đi và là công suất nơi tiêu thụ
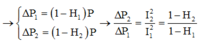
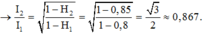
Công suất hao phí trong 2 trường hợp là 10% và 4%
Công suất tạo ra không đổi nên để hao phi giảm từ 10% xuống 4% thì có nghĩa là công suất hao phí được giảm 2,5 lần
do đó cường độ phải giảm \(\sqrt{2,5}=1,58\) lần
Do đó cần giảm cường độ đi
\(100-\frac{100}{1,58}\approx36,8\text{% }\)
\(\Rightarrow B\)
Đáp án B
Gọi số tổ máy ban đầu là n (tổ). Công suất mỗi máy là a (W). Ta có :
- Ban đầu : 
- Sau khi rút 3 tổ máy 
- Sau khi rút x tổ máy để đạt hiệu suất 95% :
Từ (1) và (2) ta có 
Từ (1) và (3) ta có 
Suy ra phải rút tổng cộng 9 tổ máy mới đạt hiệu suất 95% => phải rút thêm 6 tổ máy nữa
Giải thích: Đáp án D
Với câu này chúng ta nên nhớ công thức tính nhanh: Giữ nguyên công suất nơi tiêu thụ
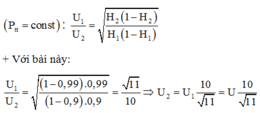
Đáp án C
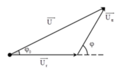
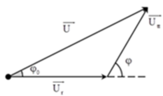
+ Ta có giản đồ vecto cho các điện áp
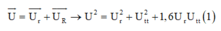
+ Mặc khác kết hợp với giả thuyết
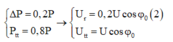
+ Thay hệ trên vào (1) ta tìm được cos φ = 5 34
+ Để giảm hao phí xuống 4 lần, nghĩa là I giảm 2 lần do vậy U r = I r cũng giảm đi hai lần
+Áp dụng định lý sin trong tam giác
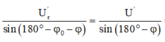
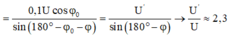
Giải thích: Đáp án A
Phương pháp:Sử dụng giản đồ vecto
Công thức tính công suất và hiệu suất
Lí thuyết về truyền tải điện năng đi xa
Cách giải: Ta có: cosφ' = 0,8
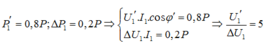
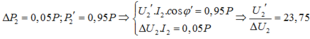
Sử dụng định lí hàm số cos:
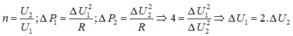
Chuẩn hoá số liệu: Cho ∆U1 = 1 => U1’ = 5
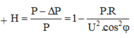
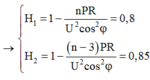
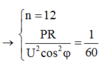
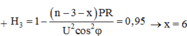
Đáp án A
Phương pháp: Áp dụng công thức tính công suất hao phí và hiệu suất truyền tải trong truyền tải điện năng đi xa
Cách giải:
+ Hiệu suất truyền tải H = P t t P = 1 - ∆ P P với P là công suất truyền đi và là công suất nơi tiêu thụ.
→ I 2 I 1 = 1 - H 2 1 - H 1 = 3 2 ≈ 0 , 867 .Giảm I đi 13,4%